题目内容
 如图,已知直线y1=k1x+b1分别与x轴,y轴交于点A、B,另一条直线y2=k2x+b2经过点C(0,1),且把△AOB分成面积相等的两部分,试分别确定两条直线的解析式.
如图,已知直线y1=k1x+b1分别与x轴,y轴交于点A、B,另一条直线y2=k2x+b2经过点C(0,1),且把△AOB分成面积相等的两部分,试分别确定两条直线的解析式.分析:利用待定系数法把A(2,0),B(0,2)代入y1=k1x+b1中可得b1=2,k1=-1,然后再根据三角形的中线平分三角形的面积可得y2=k2x+b2经过点C(0,1),A(2,0),再计算出b2=1,k2=-
,进而得到函数解析式.
| 1 |
| 2 |
解答:解:根据图象可得A(2,0),B(0,2),
∵直线y1=k1x+b1分别与x轴,y轴交于点A、B,
∴
,
解得:b1=2,k1=-1,
∴直线y1=k1x+b1的解析式为:y1=-x+2.
∵C(0,1),
∴C是OB中点,
∵另一条直线y2=k2x+b2经过点C(0,1),且把△AOB分成面积相等的两部分,
∴一条直线y2=k2x+b2经过点A(2,0),
∴
,
解得b2=1,k2=-
,
∴直线y2=k2x+b2经的解析式为:直线y2=-
x+1.
∵直线y1=k1x+b1分别与x轴,y轴交于点A、B,
∴
|
解得:b1=2,k1=-1,
∴直线y1=k1x+b1的解析式为:y1=-x+2.
∵C(0,1),
∴C是OB中点,
∵另一条直线y2=k2x+b2经过点C(0,1),且把△AOB分成面积相等的两部分,
∴一条直线y2=k2x+b2经过点A(2,0),
∴
|
解得b2=1,k2=-
| 1 |
| 2 |
∴直线y2=k2x+b2经的解析式为:直线y2=-
| 1 |
| 2 |
点评:此题主要考查了待定系数法求一次函数解析式,关键是找出两函数图象所经过的点.

练习册系列答案
相关题目
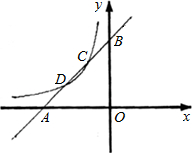 于点C、D,且C点的坐标为(-1,2).
于点C、D,且C点的坐标为(-1,2). C、D,且C点的坐标为(-1,2).
C、D,且C点的坐标为(-1,2). (2012•贵港)如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是( )
(2012•贵港)如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是( )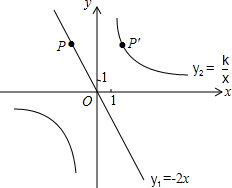 如图,已知直线y1=-2x经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y2=
如图,已知直线y1=-2x经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y2= 如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线
如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线