题目内容
 如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线y2=
如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线y2=| k | x |
(1)分别求直线AB及双曲线的解析式;
(2)根据图象分析,当x在什么范围内取值时,y1>y2?
分析:(1)把C(-1,2)代入y1=x+m得到m的值,把C(-1,2)代入双曲线y2=
(x<0)得到k的值;
(2)观察图象得到当-2<x<-1时一次函数的函数值比反比例函数的函数值要大.
| k |
| x |
(2)观察图象得到当-2<x<-1时一次函数的函数值比反比例函数的函数值要大.
解答:解:(1)把C(-1,2)代入y1=x+m,得-1+m=2,解得m=3,
∴直线的解析式为y1=x+3;
把C(-1,2)代入双曲线y2=
(x<0)得,k=-1×2=-2,
∴双曲线的解析式为y2=-
;
(2)解方程组得
得
或
,
∴D点坐标为(-2,1),
当-2<x<-1时,y1>y2.
∴直线的解析式为y1=x+3;
把C(-1,2)代入双曲线y2=
| k |
| x |
∴双曲线的解析式为y2=-
| 2 |
| x |
(2)解方程组得
|
|
|
∴D点坐标为(-2,1),
当-2<x<-1时,y1>y2.
点评:本题考查了反比例函数与一次函数图象的交点问题:把两函数的解析式联立起来组成方程组,解方程组即可得到它们的交点坐标.也考查了数形结合的思想.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
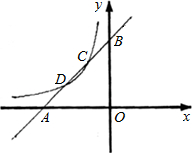 于点C、D,且C点的坐标为(-1,2).
于点C、D,且C点的坐标为(-1,2). C、D,且C点的坐标为(-1,2).
C、D,且C点的坐标为(-1,2). (2012•贵港)如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是( )
(2012•贵港)如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是( )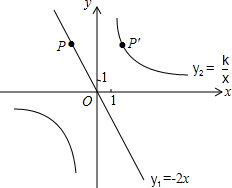 如图,已知直线y1=-2x经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y2=
如图,已知直线y1=-2x经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y2=