题目内容
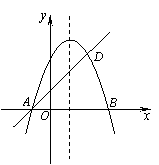
如图，抛物线y＝－x2＋bx＋c与x轴交于A、B两点，且B点的坐标为(3，0)，经过A点的直线交抛物线于点D (2， 3).
（1）求抛物线的解析式和直线AD的解析式；
（2）过x轴上的点E (a，0) 作直线EF∥AD，交抛物线于点F，是否存在实数a，使得以A、D、E、F为顶点的四边形是平行四边形？如果存在，求出满足条件的a；如果不存在，请说明理由.
 |
（1）y＝―x2＋2x＋3；A(―1，0)；y＝x＋1……………………………(4分)
（2）当
a＜－1时，DF∥AE且DF＝AE，则F点即为(0，3)，AE＝―1―a＝2，a＝－3…(6分)
当a＞－1时，显然F应在x轴下方，EF∥AD且EF＝AD，设F (a－3，－3)…(8分)
由―(a－3)2＋2(a－3
)＋3＝－3，解得a＝4±
…………………………………(10分)
综上所述，满足条件的a有三个：―3， 4±.
练习册系列答案
相关题目
______________.
?若能，求出此时∠1的度数，若不能说明理由；
AB＝1，点P是线段CD上一个动点，在AB同侧分别作等边△PAE和等边△PBF，M为线段EF的中点. 在点P从点C移动到点D时，点M运动的路径长度为 ．
分别交x轴、y轴于A、B两点，经过点A的直线m⊥x轴，直线l经过原点O交线段AB于点C，过点C作OC的垂线，与直线m相交于点P，现将直线l绕O点旋转，使交点C在线段AB上由点B向点A方向运动．
