题目内容
如图,直线y=﹣x+
 分别交x轴、y轴于A、B两点,经过点A的直线m⊥x轴,直线l经过原点O交线段AB于点C,过点C作OC的垂线,与直线m相交于点P,现将直线l绕O点旋转,使交点C在线段AB上由点B向点A方向运动.
分别交x轴、y轴于A、B两点,经过点A的直线m⊥x轴,直线l经过原点O交线段AB于点C,过点C作OC的垂线,与直线m相交于点P,现将直线l绕O点旋转,使交点C在线段AB上由点B向点A方向运动.
(1)填空:A( , )、B( , )
(2)直线DE过点C平行于x轴分别交y轴与直线m于D、E两点,求证:△ODC≌△CEP;
(3)若点C的运动速度为每秒
 单位,运动时间是t秒,设点P的坐标为(
单位,运动时间是t秒,设点P的坐标为(
 ,a)
,a)
①试写出a关于t的函数关系式和变量t的取值范围;
②当t为何值时,△PAC为等腰三角形并求出点P的坐标.


【考点】一次函数综合题.
【分析】(1)把x=0,y=0代入y=﹣x+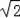
 解答即可;
解答即可;
(2)DE∥x轴,m⊥x轴,根据ASA证△ODC≌△CEP即可;
(3)①根据Rt△BDC中的勾股定理进行解答即可;
②根据等腰三角形和等腰直角三角形的性质进行解答.
【解答】解:(1)把x=0,y=0代入y=﹣x+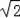
 ,可得:点A(
,可得:点A(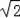
 ,0),B(0,
,0),B(0,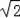
 );
);
故答案为:A(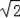
 ,0),B(0,
,0),B(0,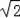
 );
);
(2)∵DE∥x轴,m⊥x轴,
∴m⊥DE,DE⊥y轴,
∴∠ODE=∠CEP=90°,
∵OC⊥CP,
∴∠OCP=90°,
∴∠DCO+∠ECP=180°﹣∠OCP=90°,
∴∠DCO+∠DOC=90°,
∴∠ECP=∠DOC,
∵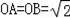
 ,
,
∴∠ABO=∠BAO,
∵DE∥x轴,
∴∠BCD=∠BAO,
∴∠ABO=∠BCD,
∴BD=CD,AE∥y轴,由平移性质得:OA=DE,
∴OB=DE,OB﹣BD=DE﹣CD,
∴OD=CE,
在△ODC与△CEP中,
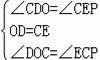
 ,
,
∴△ODC≌△CEP(ASA);
(3)①∵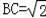
 t,BD=CD,
t,BD=CD,
在Rt△BDC中,BD2+CD2=BC2
∴BD=CD=t,OA=OB=
 ,DO=BO﹣BD=
,DO=BO﹣BD=
 ﹣t,EA=DO=
﹣t,EA=DO=
 ﹣t,
﹣t,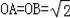
 ﹣t,EP=CD=t,AP=EA﹣EP=
﹣t,EP=CD=t,AP=EA﹣EP=
 ﹣2t,
﹣2t,
在Rt△AOB中,AO2+BO2=AB2
∴OA=2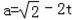
 (0≤t≤2),
(0≤t≤2),
②当t=0时,△PAC是等腰直角三角形

∴即点坐标是:P(
 ,
,
 ),PA=AC,则
),PA=AC,则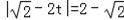
 t
t
解得t=1或t=﹣1(舍去)
∴当t=1时,△PAC是等腰三角形
即点坐标是:P(
 ,
,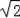
 ﹣2),
﹣2),
∴当t=0或1时,△PAC为等腰三角形,
点P的坐标为:P(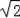
 ,
,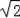
 )或P(
)或P(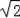
 ,
,
 ﹣2).
﹣2).
【点评】主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数的性质和点的意义表示出相应的线段的长度,再结合三角形全等和等腰三角形的性质求解.试题中贯穿了方程思想和数形结合的思想,请注意体会.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 的公因式是_______.
的公因式是_______.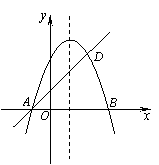
 洋的意识 D.检查一枚用于发射卫星的运载火箭的各零部件
洋的意识 D.检查一枚用于发射卫星的运载火箭的各零部件
 .
.
