题目内容
矩形ABCD中，点O是BC中点，∠AOD=90°，矩形ABCD的周长为20cm，则AB长为分析：本题运用矩形的性质通过周长的计算方法求出矩形的边长．
解答：解：矩形ABCD中，O是BC的中点，∠AOD=90°，
根据矩形的性质得到△ABO≌△DCO，则OA=OD，∠DAO=45°，
所以∠BOA=∠BAO=45°，即BC=2AB，由矩形ABCD的周长为20cm得到，20=2AB+2×2AB，
解得AB=
cm．
故答案为：
．
根据矩形的性质得到△ABO≌△DCO，则OA=OD，∠DAO=45°，
所以∠BOA=∠BAO=45°，即BC=2AB，由矩形ABCD的周长为20cm得到，20=2AB+2×2AB，
解得AB=
| 10 |
| 3 |
故答案为：
| 10 |
| 3 |
点评：本题考查矩形的性质，矩形具有平行四边形的性质，又具有自己的特性，要注意运用矩形具备而一般平行四边形不具备的性质．
练习册系列答案
一线名师提优试卷系列答案
相关题目
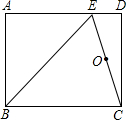如图，在矩形ABCD中，点E在AD上，EC平分∠BED．
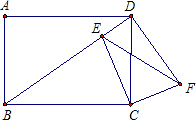如图，在矩形ABCD中，点E对角线是BD上一点，作∠CEF=∠CBD，过点C作CF⊥CE交EF于F，连接DF．求证：
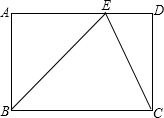如图，在矩形ABCD中，点E在AD上，CE平分∠BED．
（2012•泉港区质检）如图，在矩形ABCD中，点E是BC边上的一动点，DF⊥AE于F，连接DE．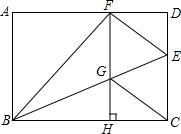
如图，在矩形ABCD中，点E为CD上一点，将△BCE沿BE翻折后点C恰好落在AD边上的点F处，过F作FH⊥BC于H，交BE于G，连接CG．