题目内容
17.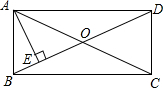 如图所示,已知在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,∠DAE:∠BAE=3:1,求∠EAC的度数.
如图所示,已知在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,∠DAE:∠BAE=3:1,求∠EAC的度数.
分析 由矩形的性质得出OA=OB,得出∠OAB=∠OBA,再由已知条件求出∠BAE=22.5°,得出∠OAB=∠OBA=67.5°,即可得出∠EAC.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∴∠OAB=∠OBA,
∵∠DAE:∠BAE=3:1,
∴∠BAE=$\frac{1}{4}$×90°=22.5°,
∵AE⊥BD,
∴∠AEB=90°,
∴∠OAB=∠OBA=90°-22.5°=67.5°,
∴∠EAC=67.5°-22.5°=45°.
点评 本题考查了矩形的性质、等腰三角形的判定与性质;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
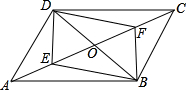 如图,在平行四边形ABCD中,已知对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向点O运动.
如图,在平行四边形ABCD中,已知对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向点O运动.