题目内容
13.若|a-1|+(b-2)2=0,求$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2013)(b+2013)}$的值.
分析 由|a-1|+(b-2)2=0,得出a=1,b=2,进一步代入分解,加减抵消得出答案即可.
解答 解:∵|a-1|+(b-2)2=0,
∴a=1,b=2,
∴原式=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$
=1-$\frac{1}{2015}$
=$\frac{2014}{2015}$.
点评 此题考查代数式求值,非负数的性质,代入后根据分数特点,运用适当的方法拆分是解决问题的关键.

练习册系列答案
相关题目
1.下面是某商场电脑产品的进货单,其中标价一栏被烧掉,请根据其他栏内的信息求出标价.
| 进价 | 标价 | 折扣 | 利润 |
| 3000 | 八折 | 200 |
5.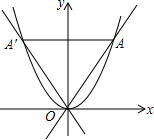 如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )
如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )
 如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )
如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )| A. | 点A′和点A关于y轴对称 | |
| B. | △AOA′是等腰三角形 | |
| C. | S△AOA′=8 | |
| D. | 线段OA绕点O逆时针旋转60°可与线段OA′重合 |
 如图.已知P为∠ABC平分线上的一点,且PE=PF,结合所学知识,
如图.已知P为∠ABC平分线上的一点,且PE=PF,结合所学知识,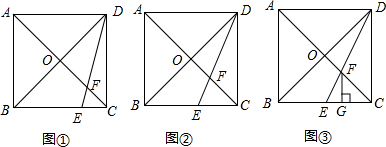
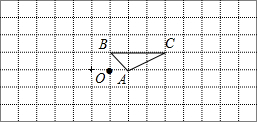 如图,在由相同的小正方形组成的网格中,△ABC的三个顶点都在小正方形的顶点处,这样的三角形称为格点三角形,现要求以点O为位似中心,将△ABC放大为原来的2倍,请你画出符合条件的格点三角形.
如图,在由相同的小正方形组成的网格中,△ABC的三个顶点都在小正方形的顶点处,这样的三角形称为格点三角形,现要求以点O为位似中心,将△ABC放大为原来的2倍,请你画出符合条件的格点三角形.