题目内容
7. 如图,一圆与平面直角坐标系中的x轴切于点A(4,0),与y轴交于点B(0,2),C(0,8),则该圆的直径为10.
如图,一圆与平面直角坐标系中的x轴切于点A(4,0),与y轴交于点B(0,2),C(0,8),则该圆的直径为10.
分析 过圆心O′作y轴的垂线,垂足为D,连接O′A,由垂径定理可知,D为BC中点,BC=16-4=12,OD=6+4=10,由切线性质可知,O′A⊥x轴,四边形OAO′D为矩形,半径O′A=OD=10,故可求得圆的直径.
解答  解:过圆心O′作y轴的垂线,垂足为D,连接O′A,
解:过圆心O′作y轴的垂线,垂足为D,连接O′A,
∵O′D⊥BC,
∴D为BC中点,
∴BC=8-2=6,OD=3+2=5,
∵⊙O′与x轴相切,
∴O′A⊥x轴,
∴四边形OAO′D为矩形,
半径O′A=OD=5,
∴圆直径是10.
故答案为:10.
点评 本题考查了切线的性质,坐标与图形的性质,垂径定理,矩形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
6.不等式3x≤2(x-1)的解集为( )
| A. | x≤-1 | B. | x≥-1 | C. | x≤-2 | D. | x≥-2 |
2. 如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
 如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )| A. | 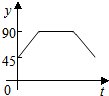 | B. | 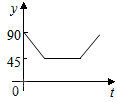 | C. | 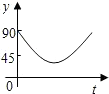 | D. | 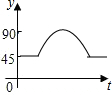 |
17. 如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )
如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )
 如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )
如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )| A. | 140 | B. | 70 | C. | 35 | D. | 24 |
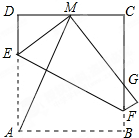 将边长为5正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.
将边长为5正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.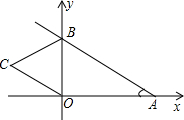 如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.
如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.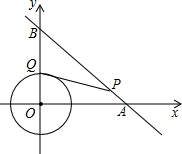 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.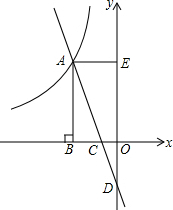 如图,直线y=kx-2与双曲线y=-$\frac{6}{x}$(x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E,△ABC的面积为2.
如图,直线y=kx-2与双曲线y=-$\frac{6}{x}$(x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E,△ABC的面积为2.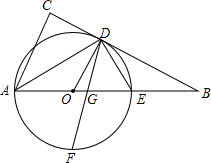 如图,E是△ABC的边AB上一点,以AE为直径的⊙O经过BC上的一点D,且OD∥AC,∠ADE的平分线DF交AB于G,交⊙O于F,且BD=BG
如图,E是△ABC的边AB上一点,以AE为直径的⊙O经过BC上的一点D,且OD∥AC,∠ADE的平分线DF交AB于G,交⊙O于F,且BD=BG