题目内容
10.阅读材料后,解答问题:解方程:(x2-1)2-5(x2-1)+4=0,
解:可设x2-1=y,即 (x2-1)2=y2,
原方程可化为 y2-5y+4=0,解得y1=1,y2=4.
当y=1即x2-1=1时,x2=2,x=±$\sqrt{2}$;
当y=4即x2-1=4时,x2=5,x=±$\sqrt{5}$;
请你依据此解法解方程:(x2-2x)2-2(x2-2x)-3=0.
分析 先设x2-2x=t,则方程即可变形为t2-2t-3=0,解方程即可求得t即x2-2x的值,再解关于x的一元二次方程即可.
解答 解:设t=x2-2x,则原方程可化为:t2-2t-3=0,
(t-3)(t+1)=0,
∴t=-1或3,
即x2-2x=-1或x2-2x=3,
解得x1=x2=1,x3=3,x4=-1.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
20.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
从上表可知,下列说法中正确的是( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | 抛物线与x轴的一个交点为(4,0) | B. | 函数y=ax2+bx+c的最大值为6 | ||
| C. | 抛物线的对称轴是x=$\frac{1}{2}$ | D. | 在对称轴右侧,y随x增大而增大 |
1.已知平面上有一点P和半径为r的⊙O,OP=d,d与r是关于x的方程x2-7x+12=0的两根,则点P与⊙O的位置关系是( )
| A. | 点P在圆外 | B. | 点P在圆内 | ||
| C. | 点P不在圆上 | D. | 点P在圆外或点P在圆内 |
18.下列四组线段中,可以构成直角三角形的是( )
| A. | 4,5,6 | B. | 6,8,10 | C. | 2,3,4 | D. | 1,1,2 |
2.若$\sqrt{{{(1-m)}^2}}$=m-1,则m的取值范围是( )
| A. | m≥1 | B. | m≤1 | C. | m=1 | D. | 一切实数 |
19.下列多项式:①x2+y2;②x2-1;③x3+4x-4;④x2-10x+25,其中能直接用公式法因式分解的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
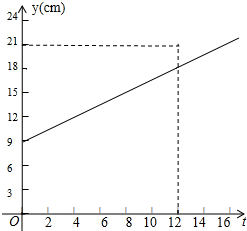 某种植物生长t天的高度为y厘米,如图反映了y与t之间的函数关系,请根据图象回答问题:
某种植物生长t天的高度为y厘米,如图反映了y与t之间的函数关系,请根据图象回答问题: