Question

11．如图，在△ABC中，点D是BC的中点，点E在边AC上，且AE：EC=2：1，AD与BE交于点F，则AF：FD=1：1，BF：FE=3：1．

Answer 1

分析 过D作DG∥BE交AC于G，由点D是BC的中点，得到BD=CD，根据平行线等分线段定理得到CG=EG，于是得到AF：FD=AE：EG=1：1，根据三角形的中位线的性质得到EF=$\frac{1}{2}$DG，DG=$\frac{1}{2}$BE，即可得到结论．

解答 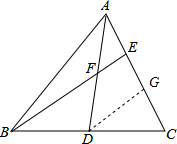解：过D作DG∥BE交AC于G，
∵点D是BC的中点，
∴BD=CD，
∴CG=EG，
∵AE：EC=2：1，
∴AE=EG=CG，
∴AF：FD=AE：EG=1：1，
∵EF=$\frac{1}{2}$DG，DG=$\frac{1}{2}$BE，
∴EF=$\frac{1}{4}$BE，
∴BF：FE=3：1，
故答案为：1：1；3：1．

点评 本题考查了平行线分线段成比例定理，本题辅助线的作法是解题的关键．