题目内容
7.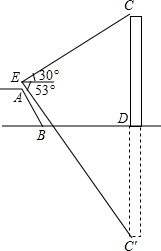 如图,斜坡AB的长为10$\sqrt{3}$米,坡度i=$\sqrt{3}$:1,小明站在斜坡顶端A处测得河对面大楼CD的楼顶点C的仰角为30°,测得点C在河中的倒影C′的俯角为53°,如果小明的眼睛E到点A的距离为1.70米,试求大楼CD的高度(结果精确到0.1米,参考数据tan53°≈1.33,sin53°≈0.80,cos53°=0.60,$\sqrt{3}$≈1.73)
如图,斜坡AB的长为10$\sqrt{3}$米,坡度i=$\sqrt{3}$:1,小明站在斜坡顶端A处测得河对面大楼CD的楼顶点C的仰角为30°,测得点C在河中的倒影C′的俯角为53°,如果小明的眼睛E到点A的距离为1.70米,试求大楼CD的高度(结果精确到0.1米,参考数据tan53°≈1.33,sin53°≈0.80,cos53°=0.60,$\sqrt{3}$≈1.73)
分析 如图,延长EA交BD于H,则EH⊥BD,过点E作EF⊥CD于F.构建直角△EFC和直角△EFC′,通过解这两个直角三角形来求CD的长度.
解答 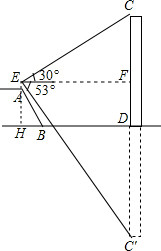 解:如图,延长EA交BD于H,则EH⊥BD,过点E作EF⊥CD于F.
解:如图,延长EA交BD于H,则EH⊥BD,过点E作EF⊥CD于F.
∵斜坡AB的长为10$\sqrt{3}$米,坡度i=$\sqrt{3}$:1,
∴$\frac{AH}{BH}$=$\sqrt{3}$,则∠ABH=60°,
∴AH=AB•sin60°=10$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=15(米).
又E到点A的距离为1.70米,
∴EH=FD=16.7米.
设CD=x,则C′D=x,
在直角△EFC中,∠CEF=30°,则EF=CF•cot30°=$\sqrt{3}$CF=$\sqrt{3}$(x-16.7).
在直角△EFC′中,∠CEF=53°,则EF=$\frac{C′F}{tan53°}$=$\frac{x+16.7}{tan53°}$,
∴$\sqrt{3}$(x-16.7)=$\frac{x+16.7}{tan53°}$,即1.73(x-16.7)=$\frac{x+16.7}{1.33}$.
解得 x≈42.4.
答:大楼CD的高度约为42.4米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,解题的关键是从题目中抽象出直角三角形并选择合适的边角关系求解.

练习册系列答案
相关题目
2.已知,当x=2时,ax3+bx+7的值是9,当x=-2时,ax3+bx+11的值是( )
| A. | 9 | B. | 5 | C. | -9 | D. | 无法确定 |
12.下列函数图象中,既是中心对称图形又是轴对称图形的是( )
| A. | 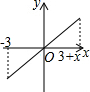 | B. | 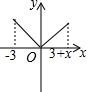 | C. | 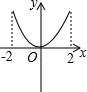 | D. | 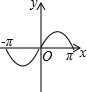 |
17.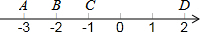 如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )
如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )
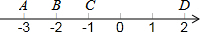 如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )
如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |