Question

13．如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度，△ABC的顶点均在格点上，三个顶点的坐标分别是A（2，2），B（1，0），C（3，1）．
（1）画出△ABC关于x轴对称的图形△A₁B₁C₁；
（2）画出将△ABC绕原点O按逆时针方向旋转90°所得作的△A₂B₂C₂，并求出C₂的坐标；
（3）在旋转过程中，点A经过的路径为弧$\widehat{A{A}_{2}}$，那么$\widehat{A{A}_{2}}$的长为$\sqrt{2}$π；
（4）△A₁B₁C₁与△A₂B₂C₂成中心对称吗？若成中心对称，写出对称中心的坐标．

Answer 1

分析 （1）利用关于x轴对称的点的坐标特征写出点A₁、B₁、C₁的坐标，然后描点即可得到△A₁B₁C₁；
（2）利用网格特点和旋转的性质画出点A₂、B₂、C₂，然后描点即可得到△A₂B₂C₂；
（3）先计算出OA，然后根据弧长公式计算；
（4）观察所画的图形，根据中心对称的定义可判断）△A₁B₁C₁与△A₂B₂C₂成中心对称，然后写出对称中心的坐标．

解答 解：（1）如图，△A₁B₁C₁为所作；
（2）如图，△A₂B₂C₂为所作，并求出C₂的坐标为（-1，3）；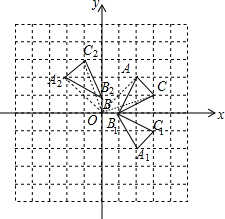

（3）OA=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$，
在旋转过程中，点A经过的路径为弧$\widehat{A{A}_{2}}$，那么$\widehat{A{A}_{2}}$的长=$\frac{90•π•2\sqrt{2}}{180}$=$\sqrt{2}$π；
（4）△A₁B₁C₁与△A₂B₂C₂成中心对称，对称中心的坐标为（$\frac{1}{2}$，$\frac{1}{2}$）．
故答案为$\sqrt{2}$π．

点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了弧长公式．