题目内容
已知矩形的一边长为6cm,对角线长为12cm,则它的周长为 cm.
考点:矩形的性质
专题:
分析:利用勾股定理列式求出另一边,再根据矩形的周长公式列式计算即可得解.
解答:解:∵矩形的一边长为6cm,对角线长为12cm,
∴矩形的另一边为
=6
cm,
∴它的周长=2(6+6
)=(12+12
)cm.
故答案为:(12+12
).
∴矩形的另一边为
| 122-62 |
| 3 |
∴它的周长=2(6+6
| 3 |
| 3 |
故答案为:(12+12
| 3 |
点评:本题考查了矩形的性质,主要利用了勾股定理,矩形的周长公式.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
当x>0,y<0时,则x,x+y,x-y中最大的数是( )
| A、x | B、x+y |
| C、x-y | D、以上答案不对 |
已知两个相似多边形的相似比是3:4,其中较小多边形的周长为36cm,则较大多边形的周长为( )
| A、48cm | B、54cm |
| C、56cm | D、64cm |
下列根式是最简二次根式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
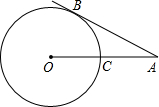 如图,AB切⊙O于B,OA交⊙O于C,∠A=30°,若⊙O半径为3cm,求AO的长.
如图,AB切⊙O于B,OA交⊙O于C,∠A=30°,若⊙O半径为3cm,求AO的长.
 在如图的网格图中按要求画出图形,并回答问题:
在如图的网格图中按要求画出图形,并回答问题: 如图所示,AB是⊙O的直径,AC是弦,DH⊥AB于H,直线DH交AC于E,点P在直线DH上,且PE=PC,求证:PC是⊙O的切线.
如图所示,AB是⊙O的直径,AC是弦,DH⊥AB于H,直线DH交AC于E,点P在直线DH上,且PE=PC,求证:PC是⊙O的切线.