题目内容
1.计算:${({-2})^2}+|{\sqrt{2}-\sqrt{3}}|-\sqrt{3}+\root{3}{-64}$.分析 原式第一项利用乘方的意义化简,第二项利用绝对值的代数意义化简,最后一项利用立方根定义计算即可得到结果.
解答 解:原式=4+$\sqrt{3}$-$\sqrt{2}$-$\sqrt{3}$-4=-$\sqrt{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
12.下列判断错误的是( )
| A. | $\frac{2}{3}$是$\frac{4}{9}$的一个平方根 | B. | $\sqrt{2}$是$\sqrt{4}$的算术平方根 | ||
| C. | 平方根等于本身的数有0和1 | D. | (-4)2的算术平方根是4 |
16.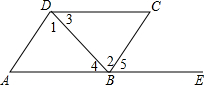 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠A=∠5 | D. | ∠A+∠ABC=180° |
6.关于x的不等式组$\left\{\begin{array}{l}{\frac{1}{3}(2x+5)>x+1}\\{\frac{1}{2}(x+3)≤x+a}\end{array}\right.$只有5个整数解,则a的取值范围是( )
| A. | 3<a<$\frac{7}{2}$ | B. | 3≤a<$\frac{7}{2}$ | C. | 3<a≤$\frac{7}{2}$ | D. | 3≤a≤$\frac{7}{2}$ |
13.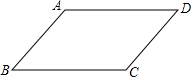 如图,下面推理中,正确的是( )
如图,下面推理中,正确的是( )
 如图,下面推理中,正确的是( )
如图,下面推理中,正确的是( )| A. | ∵∠A+∠D=180°∴AD∥BC | B. | ∵∠C+∠D=180°∴AB∥CD | ||
| C. | ∵∠A+∠D=180°∴AB∥CD | D. | ∵∠B+∠C=180°∴AD∥BC |
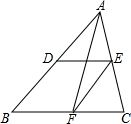 如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分.
如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分.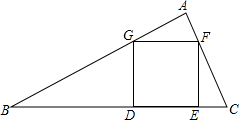 已知,如图所示,在△ABC中,正方形DEFG的顶点D,E在边BC上,另两个顶点G,F分别在边AB,AC上,且S△AGF=S△CEF=1,S△BDG=3,求S正方形DEFG.
已知,如图所示,在△ABC中,正方形DEFG的顶点D,E在边BC上,另两个顶点G,F分别在边AB,AC上,且S△AGF=S△CEF=1,S△BDG=3,求S正方形DEFG.