题目内容

9．下列给出的条件中，不能判定四边形ABCD是平行四边形的为③（填序号）
①AB=CD，AD=BC；②AD=BC，AD∥BC；③AB=CD，∠B=∠D；④AB∥CD，∠A=∠C．

分析 分别根据所给条件结合平行四边形的判定定理进行分析即可．

解答 解：①AB=CD，AD=BC可根据两组对边分别相等的四边形是平行四边形判定；
②AD=BC，AD∥BC可根据一组对边平行且相等的四边形是平行四边形进行判定；
③AB=CD，∠B=∠D不能判定四边形ABCD是平行四边形；
④AB∥CD，∠A=∠C可证出∠B=∠D，再根据两组对边分别相等的四边形是平行四边形进行判定；
故答案为：③．

点评 此题主要考查了平行四边形的判定，关键是掌握（1）两组对边分别平行的四边形是平行四边形．（2）两组对边分别相等的四边形是平行四边形．（3）一组对边平行且相等的四边形是平行四边形．（4）两组对角分别相等的四边形是平行四边形．（5）对角线互相平分的四边形是平行四边形．

练习册系列答案
相关题目
19．方程x2-3x+4=0的根的情况是（　　）
A．方程有两个不相等的实数根B．方程有两个相等的实数根
C．方程没有实数根D．无法确定
20．解方程：
（1）$\frac{x}{x-2}$-1=$\frac{8}{{x}^{2}-4}$．
（2）$\frac{x}{2x-1}$+$\frac{5}{1-2x}$=2．
17．若m＞5，则关于x的不等式（5-m）x＜2的解集为x＞$\frac{2}{5-m}$．
4．图1是边长分别为4$\sqrt{3}$和2的两个等边三角形纸片ABC和ODE叠放在一起（C与O重合）．
（1）操作：固定△ABC，将△0DE绕点C顺时针旋转30°后得到△ODE，连结AD、BE，CE的延长线交AB于F（图2）；
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论．
（2）在（1）的条件下将的△ODE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR，当点P与点F重合时停止运动（图3）
探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
（3）将图1中△0DE固定，把△ABC沿着OE方向平移，使顶点C落在OE的中点G处，设为△ABG，然后将△ABG绕点G顺时针旋转，边BG交边DE于点M，边AG交边DO于点N，设∠BGE=α（30°＜α＜90°）；（图4）
探究：在图4中，线段ON•EM的值是否随α的变化而变化？如果没有变化，请你求出ON•EM的值，如果有变化，请你说明理由．
14．义卖活动中某班以每件21元的价格购进一批商品，若每件商品售价为x元，则可卖出（350-10x）件．此班计划盈利400元，因为将商品卖给本校师生，所以限定每件商品利润不得超过20%，问每件商品售价多少元？
1．计算：${（{-2}）^2}+|{\sqrt{2}-\sqrt{3}}|-\sqrt{3}+\root{3}{-64}$．
18．下列是一元二次方程的是（　　）
A．2x2-x-3=0B．x2-2x+x3=0C．x2+y2=1D．x2+$\frac{3}{x}$=5
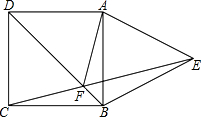19．如图，正方形ABCD中，以AB为边向形外作等边三角形ABE，连接CE，交BD于点F，连接AF．
（1）求∠BEC的度数；
（2）求∠AFD的度数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网