题目内容
4.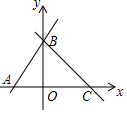 如图,在平面直角坐标系xOy中,直线AB交x轴于点A、交y轴于点B,且∠BAO=60°,直线BC垂直AB于点B,交x轴于点C,若A(-2,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线AB交x轴于点A、交y轴于点B,且∠BAO=60°,直线BC垂直AB于点B,交x轴于点C,若A(-2,0),则点C的坐标为( )| A. | (3$\sqrt{2}$,0) | B. | (6,0) | C. | (3$\sqrt{3}$,0) | D. | (5,0) |
分析 通过解直角三角形可求出OB的长度,由BC⊥AB、∠BAO=60°利用三角形内角和可得出∠BCO=30°,再通过解直角三角形可得出OC的长度,结合图形即可得出点C的坐标.
解答 解:在Rt△AOB中,∵∠AOB=90°,∠BAO=60°,A(-2,0),
∴OA=2,AB=4,OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=2$\sqrt{3}$.
∵BC⊥AB,∠BAO=60°,
∴∠BCO=30°.
在Rt△BOC中,∠BOC=90°,OB=2$\sqrt{3}$,∠BCO=30°,
∴BC=2OB=4$\sqrt{3}$,OC=$\sqrt{B{C}^{2}-O{B}^{2}}$=6,
∴点C的坐标为(6,0).
故选B.
点评 本题考查了两条直线相交或平行问题、解直角三角形以及勾股定理,通过解直角三角形求出OC的长度是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F. 补画长方体(用虚线表示被遮住的线段;只要在已有图形基础上画出长方体,不必写画法).
补画长方体(用虚线表示被遮住的线段;只要在已有图形基础上画出长方体,不必写画法).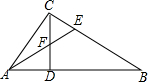 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm.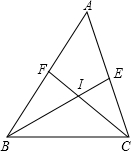 如图,在△ABC中,BE,CF是角平分线,它们相交于点I,求证:∠BIC=90°+$\frac{1}{2}$∠BAC.
如图,在△ABC中,BE,CF是角平分线,它们相交于点I,求证:∠BIC=90°+$\frac{1}{2}$∠BAC.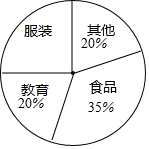 小明家下个月的开支预算如图所示.如果他家用于教育支出约为500元.那么他家下月的总支出约是多少元?用于购买食品、服装的支出分别约是多少元?
小明家下个月的开支预算如图所示.如果他家用于教育支出约为500元.那么他家下月的总支出约是多少元?用于购买食品、服装的支出分别约是多少元?