题目内容
【题目】(1)化简:(2x+1)(2x﹣1)+(x+1)(1﹣2x).
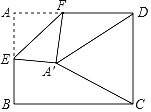
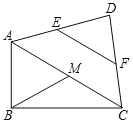
(2)如图,在四边形ABCD中,AB⊥BC,E,F,M分别是AD,DC,AC的中点,连接EF,BM,求证:EF=BM.
【答案】(1)2x2﹣x;(2)证明见解析.
【解析】
(1)原式利用平方差公式,以及多项式乘以多项式法则计算,合并即可得到结果;
(2)根据三角形的中位线定理和直角三角形斜边中线的性质可得结论.
(1)解:(2x+1)(2x-1)+(x+1)(1-2x).
=4x2-1+x-2x2+1-2x,
=2x2-x;
(2)证明:∵E,F分别是AD,DC的中点,
∴EF是△ADC的中位线,
∴EF=![]() AC,
AC,
∵AB⊥BC,M是AC的中点,
∴BM=![]() AC,
AC,
∴EF=BM.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
【题目】数学活动课上,小明同学根据学习函数的经验,对函数的图像、性质进行了探究,下面是小明同学探究过程,请补充完整:
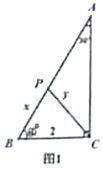
如图1,已知在![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点,连接
边上的一个动点,连接![]() .设
.设![]() ,
,![]() .
.
(初步感知)
(1)当![]() 时,则①
时,则①![]() ________,②
________,②![]() ________;
________;
(深入思考)
(2)试求![]() 与
与![]() 之间的函数关系式并写出自变量
之间的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
(3)通过取点测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 0.5 | 1 | 1.5 | 2. | 2.5 | 3 | 3.5 | 4 |
| 2 | 1.8 | 1.7 | _____ | 2 | 2.3 | 2.6 | 3.0 | _____ |
(说明:补全表格时相关数值保留一位小数)
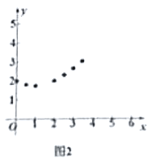
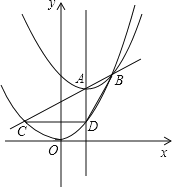
1)建立平面直角坐标系,如图2,描出已补全后的表中各对应值为坐标的点,画出该函数的图象;
2)结合画出的函数图象,写出该函数的两条性质:
①________________________________;②________________________________.