题目内容
【题目】数学活动课上,小明同学根据学习函数的经验,对函数的图像、性质进行了探究,下面是小明同学探究过程,请补充完整:
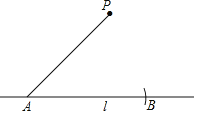
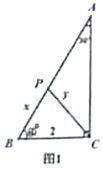
如图1,已知在![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点,连接
边上的一个动点,连接![]() .设
.设![]() ,
,![]() .
.
(初步感知)
(1)当![]() 时,则①
时,则①![]() ________,②
________,②![]() ________;
________;
(深入思考)
(2)试求![]() 与
与![]() 之间的函数关系式并写出自变量
之间的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
(3)通过取点测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 0.5 | 1 | 1.5 | 2. | 2.5 | 3 | 3.5 | 4 |
| 2 | 1.8 | 1.7 | _____ | 2 | 2.3 | 2.6 | 3.0 | _____ |
(说明:补全表格时相关数值保留一位小数)
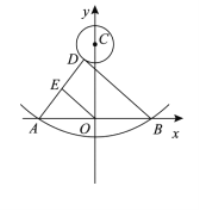
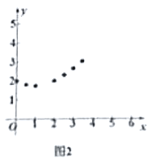
1)建立平面直角坐标系,如图2,描出已补全后的表中各对应值为坐标的点,画出该函数的图象;
2)结合画出的函数图象,写出该函数的两条性质:
①________________________________;②________________________________.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() ;(3)1.8,3.5;1)作图见解析;2)①
;(3)1.8,3.5;1)作图见解析;2)①![]() 的最小值为
的最小值为![]() (或1.7),②当
(或1.7),②当![]() 时,
时,![]() 随
随![]() 增大而减小.
增大而减小.
【解析】
(1)根据含30度直角三角形的性质求出BP,CP即可;
(2)过![]() 作
作![]() 于
于![]() ,分两种情况:①当
,分两种情况:①当![]() 时,②当
时,②当![]() 时,分别利用勾股定理计算即可;
时,分别利用勾股定理计算即可;
(3)分别求出x=1.5和x=4时y的值,即可补全表格;
1)描点、连线即可;
2)根据函数图象,可从最值和增减性方面写出函数的性质.
解:(1)当![]() 时,BP=
时,BP=![]() BC=1,CP=
BC=1,CP=![]() ,
,
故答案为:①![]() ;②
;②![]() ;
;
(2)过![]() 作
作![]() 于
于![]() ,
,
由(1)可知,![]() ,
,![]() ,
,
①当![]() 时,如图1-1,
时,如图1-1,![]() ,
,![]() ,
,
∴![]() ;
;
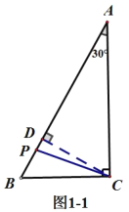
②当![]() 时,如图1-2,
时,如图1-2,![]() ,
,![]() ,
,
综合①②可得:![]()
![]() ;
;

(3)当x=1.5时,![]() ,
,
当x=4时,![]() ,
,
| 0 | 0.5 | 1 | 1.5 | 2. | 2.5 | 3 | 3.5 | 4 |
| 2 | 1.8 | 1.7 | 1.8 | 2 | 2.3 | 2.6 | 3.0 | 3.5 |
1)函数图象如图所示:
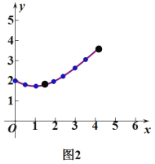
2)由函数图象得:①![]() 的最小值为
的最小值为![]() (或1.7);②当
(或1.7);②当![]() 时,
时,![]() 随
随![]() 增大而减小.
增大而减小.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计.
成绩x(分) | 频数 | 频率 |
50≤x<60 | 10 | a |
60≤x<70 | 16 | 0.08 |
70≤x<80 | b | 0.20 |
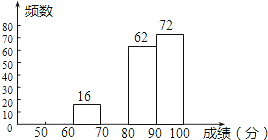
请你根据以上的信息,回答下列问题:
(1) a= ,b= ;
(2) 在扇形统计图中,“成绩x满足50≤x<60”对应扇形的圆心角大小是 ;
(3) 若将得分转化为等级,规定:50≤x<60评为D,60≤x<70评为C,70≤x<90评为B,90≤x<100评为A.这次全区八年级参加竞赛的学生约有 学生参赛成绩被评为“B”?