题目内容
2. 如图,E、F分别是正方形ABCD的边CD、AD上的点,CE=DF,AE、BF相交于点O.下列结论:(1)AE=BF;(2)AE⊥BF;(3)△ABF与△DAE成中心对称.其中,正确的结论有( )
如图,E、F分别是正方形ABCD的边CD、AD上的点,CE=DF,AE、BF相交于点O.下列结论:(1)AE=BF;(2)AE⊥BF;(3)△ABF与△DAE成中心对称.其中,正确的结论有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 只要证明△BAF≌△ADE,推出BF=AE,∠ABF=∠DAE,由∠DAE+∠BAO=90°,推出∠BAO+∠ABO=90°,推出AE⊥BF,推出①②正确,因为△ABF绕对角线的交点顺时针旋转90°可得△ADE,所以△ABF与△DAE不成中心对称,由此即可判断.
解答 解: ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=AD=CD,∠BAD=∠D=90°,
∵CE=DF,
∴AF=DE,
在△BAF和△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAD=∠D}\\{AF=DE}\end{array}\right.$,
∴△BAF≌△ADE,
∴BF=AE,∠ABF=∠DAE,
∵∠DAE+∠BAO=90°,
∴∠BAO+∠ABO=90°,
∴AE⊥BF,
∴①②正确,
∵△ABF绕对角线的交点,顺时针旋转90°可得△ADE,
∴△ABF与△DAE不成中心对称.故③错误,
故选C.
点评 本题考查全等三角形的判定和性质、正方形的性质、中心对称等知识,解题的关键是灵活运用所学知识解决问题,所以中考常考题型.

练习册系列答案
相关题目
13.-$\frac{1}{5}$的相反数是( )
| A. | -5 | B. | 5 | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
13.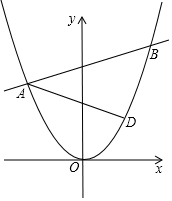 如图,点D(2,2)在抛物线y=$\frac{1}{2}$x2上,直线AB:y=kx+b交抛物线于A、B两点(A、B不与点D重合).若∠ADB=90°.求证:直线AB过定点,并求出该定点的坐标.
如图,点D(2,2)在抛物线y=$\frac{1}{2}$x2上,直线AB:y=kx+b交抛物线于A、B两点(A、B不与点D重合).若∠ADB=90°.求证:直线AB过定点,并求出该定点的坐标.
 如图,点D(2,2)在抛物线y=$\frac{1}{2}$x2上,直线AB:y=kx+b交抛物线于A、B两点(A、B不与点D重合).若∠ADB=90°.求证:直线AB过定点,并求出该定点的坐标.
如图,点D(2,2)在抛物线y=$\frac{1}{2}$x2上,直线AB:y=kx+b交抛物线于A、B两点(A、B不与点D重合).若∠ADB=90°.求证:直线AB过定点,并求出该定点的坐标.
17.函数y=kx-k的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
7.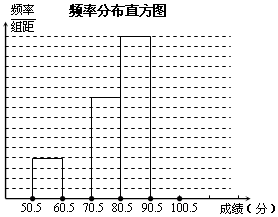 为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
频数分布表
(1)频数分布表中a=12;b=50;
(2)补全频数分布直方图;(3)在该问题中的样本容量是50;
(4)全体参赛学生中,竞赛成绩落在80.5~90.5组范围内的人数最多;
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为216人.
 为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:频数分布表
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 008 |
| 60.5~70.5 | 8 | b |
| 70.5~80.5 | 10 | 020 |
| 80.5~90.5 | 16 | 032 |
| 90.5~100.5 | a | 0.24 |
| 合计 |
(2)补全频数分布直方图;(3)在该问题中的样本容量是50;
(4)全体参赛学生中,竞赛成绩落在80.5~90.5组范围内的人数最多;
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为216人.
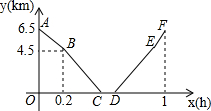 从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地,假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,小明出发时间为x(单位:h),距乙地的距离为y(单位:km),图中的折线ABCDEF表示y与x之间的函数关系.
从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地,假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,小明出发时间为x(单位:h),距乙地的距离为y(单位:km),图中的折线ABCDEF表示y与x之间的函数关系.