题目内容
某公司产销一种时令商品,每件成本20元,经行情监测得知,这种商品在未来1周的日销售量m(件)与时间t(天)的关系如表:
又知:每天的价格y(元/件)与时间t(天)的函数关系式为y=0.2t+26.8(1≤t≤7,t为整数).
(1)求未来1周的日销售量m(件)关于时间t(天)的一次函数关系式;
(2)预测未来1周中哪天的日销售利润最大,最大利润是多少?
| 时间t(天) | 1 | 3 | 6 | … |
| 日销售量m(件) | 78 | 74 | 68 | … |
(1)求未来1周的日销售量m(件)关于时间t(天)的一次函数关系式;
(2)预测未来1周中哪天的日销售利润最大,最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)设m=kt+b,由待定系数法就可以求出结论;
(2)设销售利润为w元,根据利润=销售量×每件的利润就可以表示出W与x之间的数量关系,进而化为顶点式而得出结论.
(2)设销售利润为w元,根据利润=销售量×每件的利润就可以表示出W与x之间的数量关系,进而化为顶点式而得出结论.
解答:解:(1)设m=kt+b,由题意,得
,
解得:
,
∴m=-2t+80.
∴日销售量m(件)关于时间t(天)的一次函数关系式为m=-2t+80;
(2)设销售利润为w,由题意,得
W=(-2t+80)(0.2t+26.8-20)
W=-0.4t2+24t+544,
W=-0.4(t-3)2+547.6.
∴a=-0.4<0,
∴t=3时(在1≤t≤7,t为整数的范围内),取得最大值,即第3天日销售利润最大,最大值为547.6.
|
解得:
|
∴m=-2t+80.
∴日销售量m(件)关于时间t(天)的一次函数关系式为m=-2t+80;
(2)设销售利润为w,由题意,得
W=(-2t+80)(0.2t+26.8-20)
W=-0.4t2+24t+544,
W=-0.4(t-3)2+547.6.
∴a=-0.4<0,
∴t=3时(在1≤t≤7,t为整数的范围内),取得最大值,即第3天日销售利润最大,最大值为547.6.
点评:本题考查了待定系数法求一次函数的解析式的运用,二次函数的解析式的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、x的系数是0 |
| B、24与42不是同类项 |
| C、m的次数是0 |
| D、43abc是三次单项式 |
 某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图所示),请计算所需不锈钢立柱的总长度.
某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图所示),请计算所需不锈钢立柱的总长度. 如图,在直角坐标系中,点A在x轴负半轴上,点B在x轴正半轴上,以线段AB为弦的⊙C与直线x=-2相切于点E(-2,
如图,在直角坐标系中,点A在x轴负半轴上,点B在x轴正半轴上,以线段AB为弦的⊙C与直线x=-2相切于点E(-2,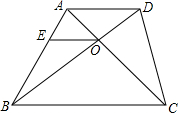 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2,
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2, 如图,梯形ABCD中,若DC∥AB,AD=BC,∠A=60°,BD⊥AD,那么∠DBA=
如图,梯形ABCD中,若DC∥AB,AD=BC,∠A=60°,BD⊥AD,那么∠DBA=