题目内容
1. 如图,在△ABC中,AB=AC,∠BAC=120°,点D在BC上,且CD=2BD,连接AD,求证:AD⊥AC.
如图,在△ABC中,AB=AC,∠BAC=120°,点D在BC上,且CD=2BD,连接AD,求证:AD⊥AC.
分析 作AE⊥BC于E,根据等腰三角形的性质得到BE=CE,∠B=∠C=°30,设BD=1,则CD=2,BC=3,BE=CE=$\frac{3}{2}$,解直角三角形得到AB=AC=$\frac{BE}{cns30°}$=$\sqrt{3}$,证得$\frac{AB}{CD}=\frac{BE}{AC}$,推出△ABE∽△DCA,根据相似三角形的性质即可得到结论.
解答 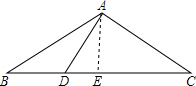 证明:作AE⊥BC于E,
证明:作AE⊥BC于E,
∵AB=AC,
∴BE=CE,∠B=∠C,
设BD=1,则CD=2,BC=3,BE=CE=$\frac{3}{2}$,
∵∠BAC=120°,
∴∠B=∠C=30°,
∴AB=AC=$\frac{BE}{cns30°}$=$\sqrt{3}$,
∵$\frac{\sqrt{3}}{2}=\frac{\frac{3}{2}}{\sqrt{3}}$,
即$\frac{AB}{CD}=\frac{BE}{AC}$,
∴△ABE∽△DCA,
∴∠DAC=∠ACB=90°,
∴AD⊥AC.
点评 本题考查了相似三角形的判定和性质,解直角三角形,等腰三角形的性质,正确的作出辅助线解题的关键.

练习册系列答案
相关题目
13.下列条件中,能作出唯一的三角形的条件是( )
| A. | 已知三边作三角形 | |
| B. | 已知两边及一角作三角形 | |
| C. | 已知两角及一边作三角形 | |
| D. | 已知一锐角和一直角边作直角三角形 |

 如图,已知A,O,E三点在同一条直线上,OB平分∠AOC,OD平分∠COE,则∠BOC与∠COD的关系为∠BOC+∠DOC=90°.
如图,已知A,O,E三点在同一条直线上,OB平分∠AOC,OD平分∠COE,则∠BOC与∠COD的关系为∠BOC+∠DOC=90°. 如图,已知D为△ABC的边BC上一点,BC=DE,∠BAD=∠CAE,∠C=∠E,∠ADB=75°.
如图,已知D为△ABC的边BC上一点,BC=DE,∠BAD=∠CAE,∠C=∠E,∠ADB=75°.