题目内容
18.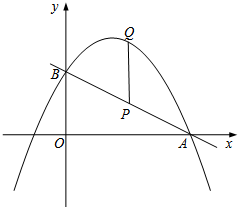 如图,直线y1=kx+2与x轴交于点A(m,0)(m>4),与y轴交于点B,抛物线y2=ax2-4ax+c(a<0)经过A,B两点.P为线段AB上一点,过点P作PQ∥y轴交抛物线于点Q.
如图,直线y1=kx+2与x轴交于点A(m,0)(m>4),与y轴交于点B,抛物线y2=ax2-4ax+c(a<0)经过A,B两点.P为线段AB上一点,过点P作PQ∥y轴交抛物线于点Q.(1)当m=5时,
①求抛物线的关系式;
②设点P的横坐标为x,用含x的代数式表示PQ的长,并求当x为何值时,PQ=$\frac{8}{5}$;
(2)若PQ长的最大值为16,试讨论关于x的一元二次方程ax2-4ax-kx=h的解的个数与h的取值范围的关系.
分析 (1)①有m=5得到A点坐标,再把A点坐标代入直线解析式求出k得到y1=-$\frac{2}{5}$x+2,接着计算自变量为0时对应的函数值可得B点坐标,然后把A点和B点坐标代入y2=ax2-4ax+c得到a和c的方程组,再解方程组求出a、c即可得到抛物线解析式;
②利用二次函数图象上点的坐标特征和一次函数图象上点的坐标特征,设点P的坐标为(x,-$\frac{2}{5}$x+2),Q(x,-$\frac{2}{5}$x2+$\frac{8}{5}$x+2),则可表示出PQ=-$\frac{5}{2}$x2+2x,然后利用PQ=$\frac{8}{5}$得到-$\frac{5}{2}$x2+2x=$\frac{8}{5}$,然后解方程即可;
(2)设P(x,kx+2),则Q(x,ax2-4ax+2),PQ的长用l表示,则易得l=ax2-(4a+k)x,再利用PQ长的最大值为16大致画出l与x的二次函数图象,由于一元二次方程ax2-4ax-kx=h的解的情况可看作为二次函数l=ax2-4ax-kx与直线l=h的交点个数,则利用函数图象可判断当h=16时,一元二次方程ax2-4ax-kx=h有两个相等的实数解;当h>16时,一元二次方程ax2-4ax-kx=h没有实数解;当0<h<16时,一元二次方程ax2-4ax-kx=h有两个解.
解答 解:(1)①∵m=5,
∴点A的坐标为(5,0),
把A(5,0)代入y1=kx+2得5k+2=0,解得k=-$\frac{2}{5}$,
∴直线解析式为y1=-$\frac{2}{5}$x+2,
当x=0时,y1=2,
∴点B的坐标为(0,2).
将A(5,0),B(0,2)代入${y_2}=a{x^2}-4ax+c$,得$\left\{\begin{array}{l}25a-20a+c=0\\ c=2.\end{array}\right.$,解得$\left\{\begin{array}{l}a=-\frac{2}{5}\\ c=2.\end{array}\right.$,
∴抛物线的表达式为y=-$\frac{2}{5}$x2+$\frac{8}{5}$x+2;
②设点P的坐标为(x,-$\frac{2}{5}$x+2),则Q(x,-$\frac{2}{5}$x2+$\frac{8}{5}$x+2),
∴PQ=-$\frac{2}{5}$x2+$\frac{8}{5}$x+2-(-$\frac{2}{5}$x+2)=-$\frac{5}{2}$x2+2x,
而PQ=$\frac{8}{5}$,
∴-$\frac{5}{2}$x2+2x=$\frac{8}{5}$,解得:x1=1,x2=4,
∴当x=1或x=4时,PQ=$\frac{8}{5}$;
(2)设P(x,kx+2),则Q(x,ax2-4ax+2),PQ的长用l表示,
∴l=ax2-4ax+2-(kx+2)=ax2-(4a+k)x,
∵PQ长的最大值为16,如图,
当h=16时,一元二次方程ax2-4ax-kx=h有两个相等的实数解;
当h>16时,一元二次方程ax2-4ax-kx=h没有实数解;
当0<h<16时,一元二次方程ax2-4ax-kx=h有两个解.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和一次函数图象上点的坐标特征;会利用待定系数法求函数解析式;理解坐标与图形性质;会利用直线与抛物线的交点个数判断方程解得情况.

| A. | (-m-2n) 2n | B. | (m-2n)(2n-m) | C. | (m-2n)(-m-2n) | D. | (2n-m)(-m-2n) |
| A. | 510×104 | B. | 51×105 | C. | 5.1×106 | D. | 0.51×107 |
912.17亿元,将912.17亿元用科学记数法表示为( )
| A. | 912.17×108 | B. | 9.1217×108 | C. | 9.1217×109 | D. | 9.1217×1010 |


 如图是由3个相同的正方体组成的一个立体图形,它的三视图是( )
如图是由3个相同的正方体组成的一个立体图形,它的三视图是( )


