题目内容
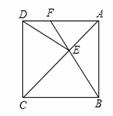
如图,在□ABCD中,E为BC边上的一点,连接AE、BD且AE=AB.
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.

证明:(1)在□ABCD中,AD∥BC,∴ ∠AEB=∠EAD.
∵ AE=AB,∴ ∠ABE=∠AEB,∴ ∠ABE=∠EAD.
(2)∵ AD∥BC,∴ ∠ADB=∠DBE.
∵ ∠ABE=∠AEB,∠AEB=2∠ADB,∴ ∠ABE=2∠ADB,
∴ ∠ABD=∠ABE-∠DBE=2∠ADB-∠ADB=∠ADB,∴ AB=AD.
又∵ 四边形ABCD是平行四边形,∴ 四边形ABCD是菱形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
校足球队10名队员的年龄情况如下:
| 年龄(单位:岁) | 12 | 13 | 14 | 15 |
| 人数 | 4 | 3 | 2 | 1 |
则这个队队员年龄的众数和平均数分别是( )
A.12, 13.1 B.12,13 C.13,13.1 D.13,13

 ,宽是
,宽是 ,一个正方形的面积等于该矩形的面积,则正方形的边长是_______.
,一个正方形的面积等于该矩形的面积,则正方形的边长是_______.
 中,
中, ∥
∥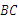 ,
, 平分∠
平分∠ ,
, ,
,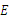 为
为 互相垂直平分.
互相垂直平分.