题目内容
如图，正方形ABCD中，点E在对角线AC上，连接EB、ED.
（1）求证：△BCE≌△DCE；
（2）延长BE交AD于点F，若∠DEB＝140º，求∠AFE的度数.
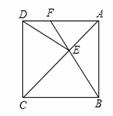
（1）证明：∵正方形ABCD中，E为对角线AC上一点，
∴BC＝DC，∠BCE＝∠DCE＝45º
又∵CE＝CE ∴△BCE≌△DCE（SAS）
（2）解：由全等可知，∠BEC＝∠DEC＝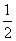
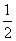∠DEB＝×140º＝70º 在△BCE中，∠CBE＝180º—70º—45º＝65º
∴在正方形ABCD中，AD∥BC，有∠AFE＝∠CBE＝65º
练习册系列答案
相关题目
的一元二次方程
时，配方后的方程可以是（ ）
B.
C.
D.
＝3，则x的值是 .
的图象恒有三个不同的交点，则常数m的取值范围是 ．某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周（按120个工时计算）生产空调、冰箱、彩电共360台，且彩电至少生产60台，已知生产这些家电产品每台所需工时和每台产值如下表：
| 家电名称 | 空调 | 冰箱 | 彩电 |
| 工时 |
|
|
|
| 产值（千元） | 4 | 3 | 2 |
问每周应生产空调、冰箱、彩电各多少台，才能使产值最高？最高产值是多少？
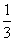
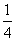
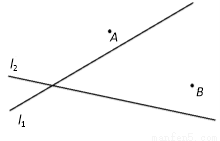
同侧、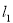
异侧的两个城镇A、B，如下图，电信部门要修建一座信号发射塔，按照设计要求，发射塔到两个城镇A、B的距离必须相等，到两条公路