题目内容
12.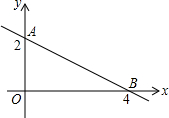 如图,直线AB与y轴,x轴的交点为A,B两点,点A,B的纵坐标、横坐标如图所示.在x轴上是否存在一点p,使S△PAB=3?若存在,求出P点的坐标,若不存在,说明理由.
如图,直线AB与y轴,x轴的交点为A,B两点,点A,B的纵坐标、横坐标如图所示.在x轴上是否存在一点p,使S△PAB=3?若存在,求出P点的坐标,若不存在,说明理由.
分析 利用三角形面积求法结合A、B点坐标进而得出答案.
解答  解:在x轴上存在一点P,使S△PAB=3,
解:在x轴上存在一点P,使S△PAB=3,
理由:如图所示:当BP=3,则S△PAB=3,
此时P(7,0),
当BP′=3,
则S△P′AB=3,
此时P′(1,0).
综上所述:符合题意的点的坐标为:(1,0),(7,0).
点评 此题主要考查了一次函数图象上点的坐标特征以及三角形面积求法,得出三角形底边长是解题关键.

练习册系列答案
相关题目
7.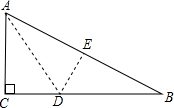 如图一直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图一直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
 如图一直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图一直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A. | 2cm | B. | 3cm | C. | 1.5cm | D. | 4cm |
17. 如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,设点A的坐标为(-3,-4)则点A′的坐标为( )
如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,设点A的坐标为(-3,-4)则点A′的坐标为( )
 如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,设点A的坐标为(-3,-4)则点A′的坐标为( )
如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,设点A的坐标为(-3,-4)则点A′的坐标为( )| A. | (3,2) | B. | (3,3) | C. | (3,4) | D. | (3,1) |
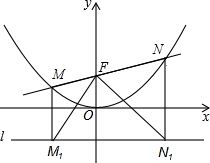 如图,过点F(0,1)的直线y=kx+b与抛物线y=$\frac{1}{4}$x2交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2>0).
如图,过点F(0,1)的直线y=kx+b与抛物线y=$\frac{1}{4}$x2交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2>0). 若∠B=40°,A、C边上任意两点,∠BAC与∠ACB的平分线交于P1,则∠P1=110°,D、F也边上任意两点,∠BFD与∠FDB的平分线交于P2,…按这样规律,则∠P2015=110°.
若∠B=40°,A、C边上任意两点,∠BAC与∠ACB的平分线交于P1,则∠P1=110°,D、F也边上任意两点,∠BFD与∠FDB的平分线交于P2,…按这样规律,则∠P2015=110°.