题目内容
14.解方程(组):(1)x2-2x-3=0;
(2)$\left\{\begin{array}{l}{x-2y=8,①}\\{x+3y=13,②}\end{array}\right.$.
分析 (1)先分解因式,即可得出两个一元一次方程,求出方程的解即可.
(2)x的系数相等,所以可以用加减法求解.
解答 解:(1)x2-2x-3=0,
(x+1)(x-3)=0,
x+1=0,x-3=0,
x1=-1,x2=3.
(2)$\left\{\begin{array}{l}{x-2y=8,①}\\{x+3y=13,②}\end{array}\right.$.
②-①得,5y=5,
解得y=1,
把y=1代入①得,x=10,
故原方程组的解为$\left\{\begin{array}{l}{x=10}\\{y=1}\end{array}\right.$.
点评 本题考查了因式分解法解一元二次方程和加减消元法解二元一次方程组,解题时要根据方程和方程组的特点选择适当的方法进行有针对性的计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,求证:△ABM为等腰三角形.
如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,求证:△ABM为等腰三角形.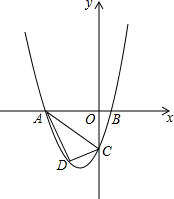 已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=4OB.
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=4OB. 一条隧道的截面由一段抛物线和一个矩形的三条边围成,矩形的长AB为20m,宽AE为2m,抛物线的最高点C到地面的距离为6m,隧道内的路面为双向行车道(正中间是一条宽2m的隔离带),一辆满载货物的汽车高为5m,宽为2m,它能安全的通过该隧道吗?请通过计算说明.
一条隧道的截面由一段抛物线和一个矩形的三条边围成,矩形的长AB为20m,宽AE为2m,抛物线的最高点C到地面的距离为6m,隧道内的路面为双向行车道(正中间是一条宽2m的隔离带),一辆满载货物的汽车高为5m,宽为2m,它能安全的通过该隧道吗?请通过计算说明. 如图,在矩形ABCD中,AB=4,BC=2,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,连接EF交边AB于点G.
如图,在矩形ABCD中,AB=4,BC=2,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,连接EF交边AB于点G. 如图,△ABC的边AB上的点D满足AC=6,AD=4,AB=9.
如图,△ABC的边AB上的点D满足AC=6,AD=4,AB=9. 的图像大致是( )
的图像大致是( ) B.
B.  C.
C.  D.
D. 
 ( )
( ) D.
D. 