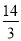题目内容
9. 一条隧道的截面由一段抛物线和一个矩形的三条边围成,矩形的长AB为20m,宽AE为2m,抛物线的最高点C到地面的距离为6m,隧道内的路面为双向行车道(正中间是一条宽2m的隔离带),一辆满载货物的汽车高为5m,宽为2m,它能安全的通过该隧道吗?请通过计算说明.
一条隧道的截面由一段抛物线和一个矩形的三条边围成,矩形的长AB为20m,宽AE为2m,抛物线的最高点C到地面的距离为6m,隧道内的路面为双向行车道(正中间是一条宽2m的隔离带),一辆满载货物的汽车高为5m,宽为2m,它能安全的通过该隧道吗?请通过计算说明.
分析 以O点为坐标原点,AB所在直线为x轴,建立坐标系,可求出抛物线的解析式,进一步代入点的坐标,求得数值比较得答案即可.
解答 解:能.
如图,以O点为坐标原点,AB所在直线为x轴,建立坐标系,
则点A(-10,0),B,10,0),C,0,4)
设抛物线的解析式为y=ax2+4,代入点A(-10,0),解得a=-0.04,
所以抛物线的方程为y=-0.04x2+4,
当x=3时,y=5.64>5,所以能通过.
点评 此题考查二次函数的实际运用,建立平面直角坐标系,求得二次函数解析式是解决问题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
19.二次函数y=m${x}^{{m}^{2}-2}$的图象有最高点,则m的值为( )
| A. | 2 | B. | 2或-2 | C. | -2 | D. | -2或-1 |
20.点A(3,y1)和点B(-2,y2)都在直线y=-4x+3上,则y1,y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
17.抛物线y=4x2向上平移3个单位是( )
| A. | y=4x2+3 | B. | y=4x2-3 | C. | y=4(x-3)2 | D. | y=4(x+3)2 |
 由8个大小相同的正方体搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体的主视图和左视图.
由8个大小相同的正方体搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体的主视图和左视图.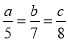 ,且3a-2b+c=3,则2a+4b-3c的值是( )
,且3a-2b+c=3,则2a+4b-3c的值是( )