题目内容
已知,在△ABC中,三条边长分别是a、b、c,且a=n2-1,b=2n,c=n2+1(n>1),求证:∠C=90°.
考点:勾股定理的逆定理
专题:证明题
分析:先求出a2+b2及c2的值,再根据勾股定理的逆定理进行解答即可.
解答:证明:∵在△ABC中,三条边长分别是a、b、c,且a=n2-1,b=2n,c=n2+1(n>1),
∴a2+b2=(n2-1)2+(2n)2=n4-2n2+1+4n2=(n2+1)2,c2=(n2+1)2,
∴a2+b2=c2,
∴∠C=90°.
∴a2+b2=(n2-1)2+(2n)2=n4-2n2+1+4n2=(n2+1)2,c2=(n2+1)2,
∴a2+b2=c2,
∴∠C=90°.
点评:本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
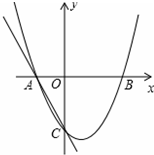 如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0)、B(2,0)两点,交y轴于点C(0,-2),过点A、C画直线.
如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0)、B(2,0)两点,交y轴于点C(0,-2),过点A、C画直线.