题目内容
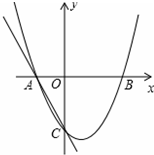 如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0)、B(2,0)两点,交y轴于点C(0,-2),过点A、C画直线.
如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0)、B(2,0)两点,交y轴于点C(0,-2),过点A、C画直线.(1)求二次函数的解析式;
(2)若点P在x轴正半轴上,且PA=PC,求OP的长.
考点:抛物线与x轴的交点,待定系数法求二次函数解析式
专题:
分析:(1)根据与x轴的两个交点A、B的坐标,设出二次函数交点式解析式y=a(x-2)(x+1),然后把点C的坐标代入计算求出a的值,即可得到二次函数解析式;
(2)设OP=x,然后表示出PC、PA的长度,在Rt△POC中,利用勾股定理列式,然后解方程即可.
(2)设OP=x,然后表示出PC、PA的长度,在Rt△POC中,利用勾股定理列式,然后解方程即可.
解答: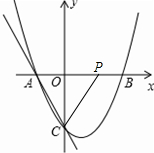 解:(1)∵二次函数y=ax2+bx+c的图象交x轴于A(-1,0)、B(2,0),
解:(1)∵二次函数y=ax2+bx+c的图象交x轴于A(-1,0)、B(2,0),
∴设该二次函数的解析式为:y=a(x-2)(x+1)(a≠0).
将x=0,y=-2代入,得-2=a(0-2)(0+1),
解得a=1,
∴抛物线的解析式为y=(x-2)(x+1),即y=x2-x-2;
(2)如图.由(1)知,抛物线的解析式为y=x2-x-2,则C(0,-2).
设OP=x,则PA=PC=x+1,
在Rt△POC中,由勾股定理,得x2+22=(x+1)2,
解得,x=
,即OP=
.
 解:(1)∵二次函数y=ax2+bx+c的图象交x轴于A(-1,0)、B(2,0),
解:(1)∵二次函数y=ax2+bx+c的图象交x轴于A(-1,0)、B(2,0),∴设该二次函数的解析式为:y=a(x-2)(x+1)(a≠0).
将x=0,y=-2代入,得-2=a(0-2)(0+1),
解得a=1,
∴抛物线的解析式为y=(x-2)(x+1),即y=x2-x-2;
(2)如图.由(1)知,抛物线的解析式为y=x2-x-2,则C(0,-2).
设OP=x,则PA=PC=x+1,
在Rt△POC中,由勾股定理,得x2+22=(x+1)2,
解得,x=
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了待定系数法求二次函数解析式,抛物线与x轴的交点.利用待定系数法求二次函数解析式时,注意合理利用抛物线解析式的三种形式.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,AB=AC,BO=CO,∠BOC=160°,求∠AOB的度数.
如图,AB=AC,BO=CO,∠BOC=160°,求∠AOB的度数. 如图,如果从半径为5cm的圆形纸片上剪去
如图,如果从半径为5cm的圆形纸片上剪去 如图,在矩形ABCD中,∠OAD=∠ODA=
如图,在矩形ABCD中,∠OAD=∠ODA= 如图,在△ABC中,角平分线AD,BE,CF交于点I,
如图,在△ABC中,角平分线AD,BE,CF交于点I,