题目内容
已知10个互不相等的有理数,每9个数的和都是分母为22的最简分数,求这10个有理数的和.
考点:有理数的加法
专题:计算题
分析:分母为22的既约真分数分子与分母无公约数的真分数,用列举法逐个尝试即可得出答案.
解答:解:这10个有理数,每9个相加,一共得出另外10个数,由于原10个有理数互不相等,
可以轻易得出它们相加后得出的另外10个数也是互不相等的,
而这10个数根据题意都是分母22的既约真分数,而满足这个条件的真分数恰好正好有10个,
∴这10项分别是:
,
,
,
,
,
,
,
,
,
,
它们每一个都是原来10个有理数其中9个相加的和,那么,如果再把这10个以22为父母的真分数相加,
得出来的结果必然是原来的10个有理数之和的9倍.
则10个真分数相加得出结果为5,于是所求的10个有理数之和为
.
可以轻易得出它们相加后得出的另外10个数也是互不相等的,
而这10个数根据题意都是分母22的既约真分数,而满足这个条件的真分数恰好正好有10个,
∴这10项分别是:
| 1 |
| 22 |
| 3 |
| 22 |
| 5 |
| 22 |
| 7 |
| 22 |
| 9 |
| 22 |
| 13 |
| 22 |
| 15 |
| 22 |
| 17 |
| 22 |
| 19 |
| 22 |
| 21 |
| 22 |
它们每一个都是原来10个有理数其中9个相加的和,那么,如果再把这10个以22为父母的真分数相加,
得出来的结果必然是原来的10个有理数之和的9倍.
则10个真分数相加得出结果为5,于是所求的10个有理数之和为
| 5 |
| 9 |
点评:此题考查了有理数的加法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
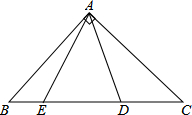 如图,△ABC中,∠BAC=90°,AB=AC,点D、E在BC上,且∠DAE=45°,求证:CD2+BE2=DE2.
如图,△ABC中,∠BAC=90°,AB=AC,点D、E在BC上,且∠DAE=45°,求证:CD2+BE2=DE2. 如图,AB=AC,BO=CO,∠BOC=160°,求∠AOB的度数.
如图,AB=AC,BO=CO,∠BOC=160°,求∠AOB的度数. 如图,如果从半径为5cm的圆形纸片上剪去
如图,如果从半径为5cm的圆形纸片上剪去 已知如图,△ABC是等腰直角三角形,AB=AC,E,F是斜边BC上的两点,且∠EAF=45°.那么以BE,EF,FC三条线段为边的正方形面积间有何关系?证明你的结论.
已知如图,△ABC是等腰直角三角形,AB=AC,E,F是斜边BC上的两点,且∠EAF=45°.那么以BE,EF,FC三条线段为边的正方形面积间有何关系?证明你的结论.