题目内容
反证法证明“三角形中至少有一个角不小于60°”先应假设这个三角形中（ ）
A.有一个内角小于60° B.每个内角都小于60°
C.有一个内角大于60° D.每个内角都大于60°
B
【解析】
试题分析：此题要运用反证法，由题意先假设三角形的三个角都小于60°成立．然后推出不成立．得出选项．
【解析】
设三角形的三个角分别为：a，b，c．
假设，a＜60°，b＜60°，c＜60°，
则a+b+c＜60°+60°+60°，
即，a+b+c＜180°与三角形内角和定理a+b+c=180°矛盾．
所以假设不成立，即三角形中至少有一个角不小于60°．
故选B．
练习册系列答案
相关题目
为半圆的直径，且
,半圆绕点B顺时针旋转45°，点
旋转到
的位置，则图中阴影部分的面积为 ．
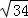C.8 D.
