Question

【题目】如图，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45°，AE、AF分别交BD于M、N，连按EN、EF、有以下结论：①AN＝EN，②当AE＝AF时，＝2﹣，③BE+DF＝EF，④存在点E、F，使得NF＞DF，其中正确的个数是（　　）

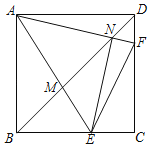
A. 1B. 2C. 3D. 4

Answer 1

【答案】B

【解析】

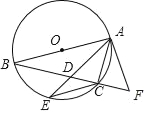
①如图1，证明△AMN∽△BME和△AMB∽△NME，可得∠NAE=∠AEN=45°，则△AEN是等腰直角三角形可作判断；
②先证明CE=CF，假设正方形边长为1，设CE=x，则BE=1-x，表示AC的长为AO+OC可作判断；
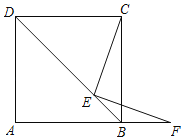
③如图3，将△ADF绕点A顺时针旋转90°得到△ABH，证明△AEF≌△AEH（SAS），则EF=EH=BE+BH=BE+DF，可作判断；
④在△ADN中根据比较对角的大小来比较边的大小．

①如图1，

∵四边形ABCD是正方形，

∴∠EBM＝∠ADM＝∠FDN＝∠ABD＝45°，

∵∠MAN＝∠EBM＝45°，∠AMN＝∠BME，

∴△AMN∽△BME，

∴，

∵∠AMB＝∠EMN，

∴△AMB∽△NME，

∴∠AEN＝∠ABD＝45°

∴∠NAE＝∠AEN＝45°，

∴△AEN是等腰直角三角形，

∴AN＝EN，

故①正确；

②在△ABE和△ADF中，

∵，

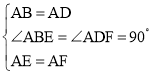∴Rt△ABE≌Rt△ADF（HL），

∴BE＝DF，

∵BC＝CD，

∴CE＝CF，

假设正方形边长为1，设CE＝x，则BE＝1﹣x，

如图2，连接AC，交EF于H，

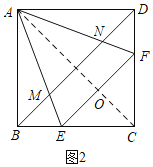
∵AE＝AF，CE＝CF，

∴AC是EF的垂直平分线，

∴AC⊥EF，OE＝OF，

Rt△CEF中，OC＝EF＝x，

△EAF中，∠EAO＝∠FAO＝22.5°＝∠BAE＝22.5°，

∴OE＝BE，

∵AE＝AE，

∴Rt△ABE≌Rt△AOE（HL），

∴AO＝AB＝1，

∴AC＝＝AO+OC，

∴1+x＝，

x＝2﹣，

∴＝＝＝；

故②不正确；

③如图3，

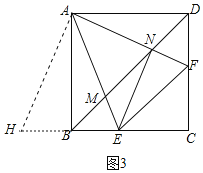
∴将△ADF绕点A顺时针旋转90°得到△ABH，则AF＝AH，∠DAF＝∠BAH，

∵∠EAF＝45°＝∠DAF+∠BAE＝∠HAE，

∵∠ABE＝∠ABH＝90°，

∴H、B、E三点共线，

在△AEF和△AEH中，

，

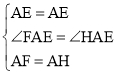∴△AEF≌△AEH（SAS），

∴EF＝EH＝BE+BH＝BE+DF，

故③正确；

④△ADN中，∠FND＝∠ADN+∠NAD＞45°，

∠FDN＝45°，

∴DF＞FN，

故存在点E、F，使得NF＞DF，

故④不正确；

故选B．