题目内容
 如图,∠B、∠D的两边分别平行.
如图,∠B、∠D的两边分别平行.(1)在图1中,∠B与∠D的数量关系是
(2)在图2中,∠B与∠D的数量关系是
(3)用一句话归纳的结论为
(4)应用:若两个角的两边两两互相平行,其中一个角的
| 1 |
| 2 |
| 1 |
| 3 |
考点:平行线的性质
专题:计算题
分析:(1)根据平行线的性质得到∠B=∠1,∠1=∠D,然后利用等量代换即可得到∠B=∠D;
(2)根据平行线的性质得到∠B=∠1,∠1+∠D=180°,然后利用等量代换即可得到∠B+∠D=180°;
(3)总结(1)和(2)的结论;
(4)设这两个角的度数分别为x,y,由于一个角的
是另一个角的
,即x=
y,则x与y不相等,x+y=180°,所以
y+y=180°,然后接方程求出y,再求x.
(2)根据平行线的性质得到∠B=∠1,∠1+∠D=180°,然后利用等量代换即可得到∠B+∠D=180°;
(3)总结(1)和(2)的结论;
(4)设这两个角的度数分别为x,y,由于一个角的
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答: 解:(1)∵AB∥CD,
解:(1)∵AB∥CD,
∴∠B=∠1,
∵BE∥DF,
∴∠1=∠D,
∴∠B=∠D;
(2)∵AB∥CD,
∴∠B=∠1,
∵BE∥DF,
∴∠1+∠D=180°,
∴∠B+∠D=180°;
(3)如果两个角的两边分别平行,那么这两个角相等或互补;证明见(1)和(2);
故答案为相等,互补,如果两个角的两边分别平行,那么这两个角相等或互补;
(4)设这两个角的度数分别为x,y,
∵一个角的
是另一个角的
,
∴
x=
y,即x=
y,
∴x与y不相等,
∴x+y=180°,
∴
y+y=180°,解得y=108°,
∴x=72°,
即这两个角的度数分别为72°、108°.
 解:(1)∵AB∥CD,
解:(1)∵AB∥CD,∴∠B=∠1,
∵BE∥DF,
∴∠1=∠D,
∴∠B=∠D;
(2)∵AB∥CD,
∴∠B=∠1,
∵BE∥DF,
∴∠1+∠D=180°,
∴∠B+∠D=180°;
(3)如果两个角的两边分别平行,那么这两个角相等或互补;证明见(1)和(2);
故答案为相等,互补,如果两个角的两边分别平行,那么这两个角相等或互补;
(4)设这两个角的度数分别为x,y,
∵一个角的
| 1 |
| 2 |
| 1 |
| 3 |
∴
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
∴x与y不相等,
∴x+y=180°,
∴
| 2 |
| 3 |
∴x=72°,
即这两个角的度数分别为72°、108°.
点评:本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
相关题目
 观察下面四幅图案中,能通过如图平移得到的是( )
观察下面四幅图案中,能通过如图平移得到的是( )A、 |
B、 |
C、 |
D、 |
 如图,O为?ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S□ABCD=12,则S△DOE的值为( )
如图,O为?ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S□ABCD=12,则S△DOE的值为( )| A、1 | B、1.5 | C、2 | D、2.25 |
下列计算正确的是( )
| A、a3+a2=2a5 |
| B、(2a3)2=4a6 |
| C、(a+b)2=a2+b2 |
| D、a6÷a2=a3 |
 在平面直角坐标系xOy中,抛物线y=-x2-(m-1)x+m2-6交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC.
在平面直角坐标系xOy中,抛物线y=-x2-(m-1)x+m2-6交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC. 如图,已知A、B、D在一条直线上,且BC∥DE,∠DEB=∠C,则AC与BE平行吗?试说明理由.
如图,已知A、B、D在一条直线上,且BC∥DE,∠DEB=∠C,则AC与BE平行吗?试说明理由.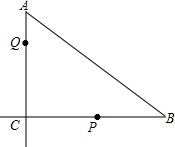 如图,在Rt△ABC中,∠BCA=90°,AC=6cm,BC=8cm.有一动点P从B点出发,在射线BC方向移动,速度是2cm/s,在P点出发后2秒后另一个动点Q从A点出发,在射线AC方向移动,速度是1cm/s.若设P出发后时间为t秒.
如图,在Rt△ABC中,∠BCA=90°,AC=6cm,BC=8cm.有一动点P从B点出发,在射线BC方向移动,速度是2cm/s,在P点出发后2秒后另一个动点Q从A点出发,在射线AC方向移动,速度是1cm/s.若设P出发后时间为t秒.