题目内容
4.一个不透明的袋子里有5个红球和3个黄球,这些球除颜色外完全相同,从袋子中随机摸出一个球,它是红球的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
分析 由一个不透明的袋子里有5个红球和3个黄球,这些球除颜色外完全相同,直接利用概率公式求解即可求得答案.
解答 解:∵一个不透明的袋子里有5个红球和3个黄球,这些球除颜色外完全相同,
∴从袋子中随机摸出一个球,它是红球的概率是:$\frac{5}{8}$.
故选:D.
点评 此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.函数y=$\sqrt{x-2}$的自变量的取值范围是( )
| A. | x≠2 | B. | x=2 | C. | x≤2 | D. | x≥2 |
16.先化简,再求代数式的值:($\frac{2}{a+1}$+$\frac{a+2}{{a}^{2}-1}$)÷$\frac{a}{a-1}$=( ),其中a=tan60°-2sin30°.
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{7}$ | D. | $\sqrt{5}$ |
16.若二次函数y=x2-6x+c的图象过A(-1,y1),B(2,y2),C(3,y3),则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y1>y3 | D. | y3>y1>y2 |
 为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,则这棵古杉树AB的长为18m.(结果取整数)(参考数据:$\sqrt{2}$=1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,则这棵古杉树AB的长为18m.(结果取整数)(参考数据:$\sqrt{2}$=1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)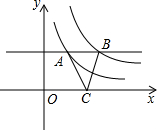 如图是反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A,B两点,点C为x轴上一点,若S△ABC=3,则k2-k1的值是( )
如图是反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A,B两点,点C为x轴上一点,若S△ABC=3,则k2-k1的值是( )