题目内容
15.运用适当的方法解方程(1)2(x-3)2=8
(2)4x2-6x-3=0
(3)(2x-3)2=5(2x-3)
(4)(x+8)(x+1)=-12.
分析 (1)两边除以2后开方,即可得出两个一元一次方程,求出方程的解即可;
(2)求出b2-4ac的值,再代入公式求出即可;
(3)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(4)整理后分解因式,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)2(x-3)2=8,
(x-3)2=4,
x-3=±2,
x1=5,x2=1;
(2)4x2-6x-3=0,
b2-4ac=(-6)2-4×4×(-3)=84,
x=$\frac{6±\sqrt{84}}{2×4}$,
x1=$\frac{3+\sqrt{21}}{4}$,x2=$\frac{3-\sqrt{21}}{4}$;
(3)(2x-3)2=5(2x-3),
(2x-3)2-5(2x-3)=0,
(2x-3)(2x-3-5)=0,
2x-3=0,2x-3-5=0,
x1=$\frac{3}{2}$,x2=4;
(4)(x+8)(x+1)=-12,
整理得:x2+9x+20=0,
(x+4)(x+5)=0,
x+4=0,x+5=0,
x1=-4,x2=-5.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
相关题目
10.请先将下列各数中需要化简的数化简,然后将原来六个数按从小到大的顺序排列,并用“<”依次连接.
33,(-2)3,0,|-$\frac{1}{2}$|,-$\frac{1}{10}$,(-1)10.
33,(-2)3,0,|-$\frac{1}{2}$|,-$\frac{1}{10}$,(-1)10.
5.若点A(a,b)在第二象限,则点B(-a,b+1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图是由八个相同的小正方体组合而成的几何体,从正面看到的图形是( )
如图是由八个相同的小正方体组合而成的几何体,从正面看到的图形是( )



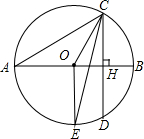 如图,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.
如图,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H. 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD. 如图所示,A(4,2),P在y轴上,∠PAO=45°,求P的坐标.
如图所示,A(4,2),P在y轴上,∠PAO=45°,求P的坐标.