Question

【题目】已知抛物线与轴交于点。

（1）抛物线的顶点坐标为_____________，点坐标为____________；（用含的代数式表示）；

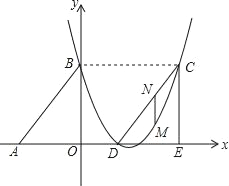
（2）当时，抛物线上有一动点，设点横坐标为，且。

①若点到轴的距离为2时，求点的坐标；

②设抛物线在点与点之间部分（含点和点）最高点与最低点纵坐标之差为，求与之间的函数关系式，并写出自变量的取值范围；

（3）若点，连结，当抛物线与线段只有一个交点时，直接写出的取值范围。

Answer 1

【答案】（1）顶点，点；（2）①或；②；（3）或.

【解析】

（1）把抛物线配方成顶点式即得抛物线的顶点坐标；求当x=0时对应的y值即可得出点C坐标；

（2）①先把m=1代入即得抛物线的解析式，进而可表示出点P的坐标，然后根据点到轴的距离为2可得关于n的方程，解方程即可求得结果；

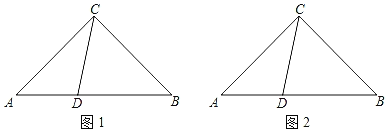
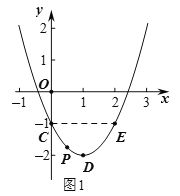
②先求得点P、C和顶点D的坐标，再结合图象：如图1、2、3，分情况讨论写出即可；

（3）根据题意，先求出抛物线与直线y=2的两个交点，然后结合图象即可得出m须满足的不等式组，解不等式组即可求出结果.

解：（1），当x=0时，，

∴顶点，点；

（2）①当时，，∴，

令，解得，∴，

令，解得，（舍），∴，

综上：点P坐标是或；

②，顶点D的坐标，

当时，如图1，；

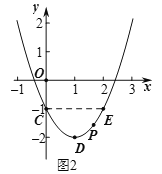
当时，如图2，；

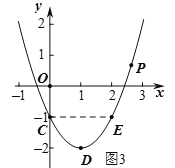
当时，如图3，；

综上，与之间的函数关系式是：；

（3）∵，∴AB∥x轴，

当y=2时，，解得：，即抛物线与直线y=2的两个交点为与，

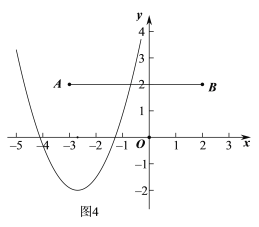
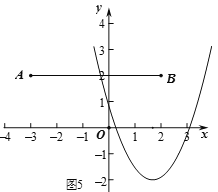
因为抛物线与线段只有一个交点，如图4、图5，

所以m须满足：或，

解得：或.