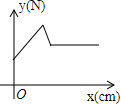题目内容
3.填出下列一元二次方程的根(1)x(x-3)=0.x1=0,x2=3
(2)(2x-7)(x+2)=0.x1=3.5,x2=-2
(3)3x2=2x.x1=0,x2=$\frac{2}{3}$
(4)x2+6x+9=0.x1=x2=-3
(5)$\sqrt{2}$x2-2$\sqrt{3}$x=0x1=0,x2=$\sqrt{6}$
(6)(1+$\sqrt{2}$)x2=(1-$\sqrt{2}$)xx1=0,x2=2$\sqrt{2}$-3
(7)(x-1)2-2(x-1)=0.x1=1,x2=3.
(8)(x-1)2-2(x-1)=-1.x1=x2=2.
分析 (1)方程利用因式分解法求出解即可;
(2)方程利用因式分解法求出解即可;
(3)方程整理后,利用因式分解法求出解即可;
(4)方程整理后,利用因式分解法求出解即可;
(5)方程整理后,利用因式分解法求出解即可;
(6)方程整理后,利用因式分解法求出解即可;
(7)方程整理后,利用因式分解法求出解即可;
(8)方程整理后,利用因式分解法求出解即可.
解答 解:(1)方程x(x-3)=0,
可得x=0或x-3=0,
解得:x1=0,x2=3;
(2)方程(2x-7)(x+2)=0,
可得2x-7=0或x+2=0,
解得:x1=3.5,x2=-2;
(3)方程整理得:x(3x-2)=0,
可得x=0或3x-2=0,
解得:x1=0,x2=$\frac{2}{3}$;
(4)方程整理得:(x+3)2=0,
解得:x1=x2=-3;
(5)分解因式得:x($\sqrt{2}$x-2$\sqrt{3}$)=0,
解得:x1=0,x2=$\sqrt{6}$;
(6)方程整理得:x[(1+$\sqrt{2}$x)-(1-$\sqrt{2}$)]=0,
解得:x1=0,x2=2$\sqrt{2}$-3;
(7)分解因式得:(x-1)(x-1-2)=0,
解得:x1=1,x2=3;
(8)方程整理得:(x-2)2=0,
解得:x1=x2=2.
故答案为:(1)x1=0,x2=3;(2)x1=3.5,x2=-2;(3)x1=0,x2=$\frac{2}{3}$;(4)x1=x2=-3; (5)x1=0,x2=$\sqrt{6}$;(6)x1=0,x2=2$\sqrt{2}$-3;(7)x1=1,x2=3;(8)x1=x2=2.
点评 此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
14.用公式法解一元二次方程${x^2}-\frac{1}{4}=2x$,正确的应是( )
| A. | $x=\frac{{-2±\sqrt{5}}}{2}$ | B. | $x=\frac{{2±\sqrt{5}}}{2}$ | C. | $x=\frac{{1±\sqrt{5}}}{2}$ | D. | $x=\frac{{1±\sqrt{3}}}{2}$ |
18.下列方程中有两个相等实数根的是( )
| A. | 7x2-x-1=0 | B. | 9x2=4(3x-1) | C. | x2+7x+15=0 | D. | 2x2-$\sqrt{3}$x-2=0 |
8.下列各组的三条线段中,不能组成三角形的是( )
| A. | 2,2,1 | B. | 5,2,4 | C. | 1,1,2 | D. | 5,6,7 |
13.在9,$\sqrt{3}$,$\frac{3}{16}$,-0.1这四个数中,是无理数的是( )
| A. | 9 | B. | $\sqrt{3}$ | C. | $\frac{3}{16}$ | D. | -0.1 |
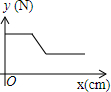
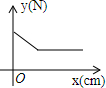
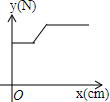
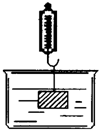 如图,在物理实验课上,小明用弹簧秤将铁块A从完全置身水槽外,到匀速向下放入盛有水的水槽中,直至铁块完全浸入水面下的一定深度,则图能反映弹簧秤的读数y(单位:N)与铁块下降的高度x(单位:cm)之间的函数关系的大致图象是( )
如图,在物理实验课上,小明用弹簧秤将铁块A从完全置身水槽外,到匀速向下放入盛有水的水槽中,直至铁块完全浸入水面下的一定深度,则图能反映弹簧秤的读数y(单位:N)与铁块下降的高度x(单位:cm)之间的函数关系的大致图象是( )