题目内容
6. 在正方形ABCD的外侧作直线AP,过点B作BO⊥AP,垂足为O.
在正方形ABCD的外侧作直线AP,过点B作BO⊥AP,垂足为O.(1)在图中画出△ABO关于直线AP对称的△AEO;
(2)在(1)的条件下,连结DE.
①当∠PAB=20°时,求∠ADE的度数;
②当∠PAB=α,且0°<α<90°(α≠45°)时,直接写出△ADE中∠ADE的度数(结果可用含α的代数式表示).
分析 (1)根据题意直接画出图形得出即可;
(2)①利用对称的性质以及等角对等边进而得出答案;
②由轴对称的性质可得:∠PAB=∠PAE=α,AE=AB=AD,分两种情况分别用等腰三角形的性质和平角以及周角的意义计算即可.
解答 解:(1)如图1所示:
(2)①由对称得∠PAB=∠PAE=20°,AE=AB=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAP=∠BAP=20°,
∴∠EAD=130°,
∴∠ADE=$\frac{180°-130°}{2}$=25°;
②Ⅰ、当0°<α<45°时,如图1,由对称得∠PAB=∠PAE=α,AE=AB=AD,
∴∠BAE=2∠PAB=2α,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠DAE=∠BAD+∠BAE=∠BAD+2∠BAP=90°+2α,
∵AE=AB,
∴∠ADE=$\frac{1}{2}$(180°-∠DAE)=$\frac{1}{2}$[180°-(90°+2α)]=45°-α;
Ⅱ、当45°<α<90°时,如图2,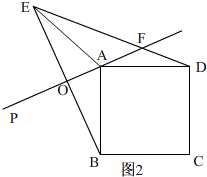
由对称得∠PAB=∠PAE=α,AE=AB=AD,
∴∠BAE=2∠PAB=2α
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠DAE=360°-∠BAD-2∠BAP=360°-90°-2α=270°-2α,
∵AE=AB,
∴∠ADE=$\frac{1}{2}$(180°-∠DAE)=$\frac{1}{2}$[180°-(270°-2α)]=α-45°.
∴当0°<α<45°时,∠ADE=45°-α,当45°<α<90°时,∠ADE=α-45°.
点评 此题主要考查了正方形的性质以及平角,周角的意义和等腰三角形的性质等知识,利用轴对称的性质得出对应边相等是解题关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
16.在有25名男生和20名女生的班级中,随机抽取一名学生做代表,则下列说法正确的是( )
| A. | 男、女生做代表的可能性一样大 | |
| B. | 男生做代表的可能性大 | |
| C. | 女生做代表的可能性大 | |
| D. | 男、女生做代表的可能性大小不能确定 |
14.某计算器每个定价80元,若购买不超过20个,则按原价付款:若一次购买超过20个,则超过部分按七折付款.设一次购买数量为x(x>20)个,付款金额为y元,则y与x之间的表达式为( )
| A. | y=0.7×80(x-20)+80×20 | B. | y=0.7x+80(x-10) | ||
| C. | y=0.7×80•x | D. | y=0.7×80(x-10) |
1.已知P=60×104×20,则P可用科学记数法表示为( )
| A. | 1.2×108 | B. | 1.2×107 | C. | 1.2×106 | D. | 12×106 |
11.在方程2(x+y)-3(y-x)=3中,用含x的式子表示y,则( )
| A. | y=5x-3 | B. | y=-x-3 | C. | $y=\frac{3x-2}{2}$ | D. | y=5x+3 |
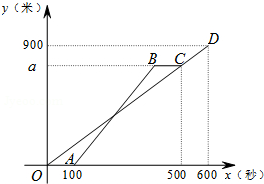 甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.
甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.