题目内容
 如图,△ABC和△A′B′C′中,AB=A′B′,BC=B′C′,点D、D′分别是BC、B′C′的中点,且AD=A′D′,求证:∠B=∠B′.
如图,△ABC和△A′B′C′中,AB=A′B′,BC=B′C′,点D、D′分别是BC、B′C′的中点,且AD=A′D′,求证:∠B=∠B′.考点:全等三角形的判定与性质
专题:证明题
分析:由D与D′分别为BC,B′C′的中点,且BC=B′C′,得到BD=B′D′,利用SSS得到△ABD≌△A′B′D′,利用全等三角形对应角相等即可得证.
解答:证明:∵BC=B′C′,点D、D′分别是BC、B′C′的中点,
∴BD=DC=
BC,B′D′=D′C′=
B′C′,即BD=B′D′,
在△ABD和△A′B′D′中,
,
∴△ABD≌△A′B′D′,
∴∠B=∠B′.
∴BD=DC=
| 1 |
| 2 |
| 1 |
| 2 |
在△ABD和△A′B′D′中,
|
∴△ABD≌△A′B′D′,
∴∠B=∠B′.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
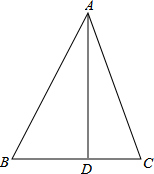 如图,在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,∠BAC=45°,AD⊥BC于点D,BD=3,CD=2.
如图,在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,∠BAC=45°,AD⊥BC于点D,BD=3,CD=2. 如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.
如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.