题目内容
12.解下列方程组(或不等式组)(1)$\left\{\begin{array}{l}{3x+y=16}\\{5x-2y=23}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x+1}{4}=\frac{y+2}{3}}\\{3(x-3)+2y=2}\end{array}\right.$
(3)解不等式$\frac{x-3}{4}$<6-$\frac{3-4x}{2}$,并把解集在数轴上表示出来.
(4)求不等式组$\left\{\begin{array}{l}{2x-3<9-x}\\{-\frac{3}{2}≤x-\frac{5}{2}}\end{array}\right.$的解集,并写出其所有整数解.
分析 (1)方程组中两方程变形后,相加消去y求出x的值,进而求出y的值,即可求出方程组的解;
(2)方程组中两方程变形后,相加消去x求出y的值,进而求出x的值,即可求出方程组的解;
(3)首先去分母,移项,合并同类项,然后把x的系数化成1,即可求解.
(4)分别求出不等式组中两不等式的解集,找出解集的公共部分,求出不等式组的解集,找出解集中的整数解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x+y=16①}\\{5x-2y=23②}\end{array}\right.$,
①×2+②得:11x=55,即x=5,
将x=5代入①得:15+y=16,即y=1,
则方程组的解为 $\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$;
(2)原方程组化为$\left\{\begin{array}{l}{3x-4y=5①}\\{3x+2y=11②}\end{array}\right.$,
②-①得:6y=6,即y=1,
将y=1代入①得:3x-4=5,即x=3,
则方程组的解为 $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$;
(3)x-3<24-2(3-4x),
x-3<24-6+8x,
x-8x<24-6+3,
-7x<21,
x>-3.
此不等式的解集在数轴上表示如下:
(4)$\left\{\begin{array}{l}{2x-3<9-x①}\\{-\frac{3}{2}≤x-\frac{5}{2}②}\end{array}\right.$,
由①得:x<4,
由②得:x≥1,
∴不等式组的解集为:1≤x<4,
则整数解1、2、3.
点评 本题考查的是解一元一次不等式组及解二元一次方程组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

 名师点拨卷系列答案
名师点拨卷系列答案 如图,在平面直角坐标系中,点A1、A2、A3,…是x轴正半轴上的点,且OA1=A1A2=A2A3=…,分别过点A1、A2、A3,…作y轴的平行线,交反比例函数y=$\frac{6}{x}$(x>0)的图象于点B1、B2、B3,…,则△AnBnBn+1的面积等于( )
如图,在平面直角坐标系中,点A1、A2、A3,…是x轴正半轴上的点,且OA1=A1A2=A2A3=…,分别过点A1、A2、A3,…作y轴的平行线,交反比例函数y=$\frac{6}{x}$(x>0)的图象于点B1、B2、B3,…,则△AnBnBn+1的面积等于( )| A. | $\frac{3}{n}$ | B. | $\frac{6}{n}$ | C. | $\frac{3}{n+1}$ | D. | $\frac{6}{n+1}$ |
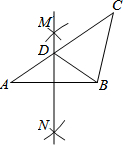 如图,在△ABC中,按以下步骤作图:①分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠C=44°,则∠A等于( )
如图,在△ABC中,按以下步骤作图:①分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠C=44°,则∠A等于( )| A. | 35° | B. | 34° | C. | 32° | D. | 30° |
| A. | 多边形的内角中锐角的个数最少有4个 | |
| B. | 多边形的内角中锐角的个数最少有3个 | |
| C. | 多边形的内角中锐角的个数最少有2个 | |
| D. | 多边形的内角中锐角的个数最多有2个 |
| A. | 内错角不相等,两直线不平行 | B. | 一个角的余角一定大于这个角 | ||
| C. | 一个钝角的补角必是锐角 | D. | 过两点有且只有一条直线 |
 如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是2;数轴上到原点的距离等于2的点所表示的数是-2和2.
如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是2;数轴上到原点的距离等于2的点所表示的数是-2和2.