题目内容
7．
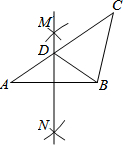如图，在△ABC中，按以下步骤作图：①分别以点A，B为圆心，大于$\frac{1}{2}$AB的长为半径画弧，相交于两点M，N；②作直线MN交AC于点D，连接BD．若CD=BC，∠C=44°，则∠A等于（ ）| A． | 35° | B． | 34° | C． | 32° | D． | 30° |
分析 直接利用线段垂直平分线的性质得出∠DAB=∠ABD，进而结合三角形外角的性质进而得出答案．
解答 解：由题意可得：MN垂直平分AB，
则AD=BD，
故∠DAB=∠ABD，
∵DC=BC，
∴∠CDB=∠CBD，
∵∠C=44°，
∴∠CDB=∠CBD=68°，
∴∠A=∠ABD=34°．
故选：B．
点评 此题主要考查了线段垂直平分线的作法与性质，正确得出∠DAB=∠ABD是解题关键．
练习册系列答案
相关题目
17．10名射击运动员第一轮比赛的成绩如表所示：
则他们本轮比赛的平均成绩是8.4（环）
| 环数 | 7 | 8 | 9 | 10 |
| 人数 | 3 | 2 | 3 | 2 |
为了解初三学生的体育锻炼时间，小华调查了某班45名同学一周参加体育锻炼的情况，并把它绘制成折线统计图．由图可知，一周参加体育锻炼时间等于9小时的人数是（ ）
15．对多项式a2-1因式分解，正确的是（ ）
| A． | a2-1=（a+1）2 | B． | a2-1=（a-1）2 | C． | a2-1=（a-1）（a+1） | D． | a2-1=（1-a）（1+a） |
2．
在△ABC中，EF是线段AC的垂直平分线，AF=12，BF=3，则BC=（ ）
在△ABC中，EF是线段AC的垂直平分线，AF=12，BF=3，则BC=（ ）| A． | 3 | B． | 12 | C． | 15 | D． | 9 |
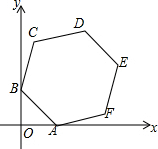如图，正六边形ABCDEF的边长为4，两顶点A，B分别在x轴和y轴上运动，则顶点D到原点O的距离的最大值为2+2$\sqrt{13}$；最小值为2$\sqrt{13}$-2．