题目内容
11. 如图,点A(m,m+1),B(m+3,m-1)是反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的交点,当反比例函数的函数值大于一次函数的函数值时,x的取值范围是0<x<3或x>6.
如图,点A(m,m+1),B(m+3,m-1)是反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的交点,当反比例函数的函数值大于一次函数的函数值时,x的取值范围是0<x<3或x>6.
分析 根据反比例函数图象上点的坐标特征列出方程,求出m的值,得到点A、B的坐标,结合图象解答即可.
解答 解:∵点A(m,m+1),B(m+3,m-1)是反比例函数y=$\frac{k}{x}$(x>0)图象上的点,
∴m(m+1)=(m+3)(m-1),
解得,m=3,
则点A的坐标为(3,4),B(6,2),
由图象可知,当0<x<3或x>6时,反比例函数的函数值大于一次函数的函数值,
故答案为:0<x<3或x>6.
点评 本题考查的是一次函数与反比例函数的交点问题,掌握反比例函数图象上点的坐标特征、灵活运用数形结合思想是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
4.在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
| A. | 平均数为160 | B. | 中位数为158 | C. | 众数为158 | D. | 方差为20.3 |
19.在-5,0,3,-2这四个数中,绝对值最小的数是( )
| A. | -5 | B. | 0 | C. | 3 | D. | -2 |
6.下列式子中,正确的是( )
| A. | $\root{3}{-8}=-\root{3}{8}$ | B. | $-\sqrt{3.6}=-0.6$ | C. | $\sqrt{{{(-3)}^2}}=-3$ | D. | $\sqrt{36}=±6$ |
16.一种计算机每秒可做40×107次运算,用科学记数法表示它工作30×102秒运算的次数为( )
| A. | 1.2×1012 | B. | 12×1024 | C. | 12×1012 | D. | 12×108 |
 已知线段a和b,求作线段AB,使AB=2a-b.(不写作法,保留作图痕迹)
已知线段a和b,求作线段AB,使AB=2a-b.(不写作法,保留作图痕迹)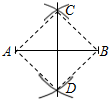 老师在黑板上作线段AB的垂直平分线,步骤如下:分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于C、D,如图,根据他的作图方法可知四边形ADBC一定是( )
老师在黑板上作线段AB的垂直平分线,步骤如下:分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于C、D,如图,根据他的作图方法可知四边形ADBC一定是( )