题目内容
 两个反比例函数y=
两个反比例函数y=| 3 |
| x |
| 6 |
| x |
| 6 |
| x |
| 3 |
| x |
| 4021 |
| 2 |
| 4021 |
| 2 |
分析:本题主要是找规律,找出规律即可得到本题答案,先根据已知条件,可先求得当y分别为1,3,5时所对应的x的值,即可得出当y=2005时的x的值,再将其代入y=
即可得出y2011的值.
| 3 |
| x |
解答:解:根据已知给出的条件,
连续代入便寻找出规律,
当y分别为1,3,5,…2011时,x1,x2,x3,…,x2011,
分别为6,2,
,…,
,
再将x1,x2,x3,…,x2011,
分别代入y=
,
得:y1,y2,y3,…,y2011,
分别为
,
,
,…,
,
∴则y2011=
,
故答案为:
.
连续代入便寻找出规律,
当y分别为1,3,5,…2011时,x1,x2,x3,…,x2011,
分别为6,2,
| 6 |
| 5 |
| 6 |
| 2011 |
再将x1,x2,x3,…,x2011,
分别代入y=
| 3 |
| x |
得:y1,y2,y3,…,y2011,
分别为
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 4021 |
| 2 |
∴则y2011=
| 4021 |
| 2 |
故答案为:
| 4021 |
| 2 |
点评:本题考查了反比例函数的性质,并且本题具有一定的规律性,要求解本题,找出规律是关键,要求学生在今后的学习中认真分析、总结所遇到的规律性问题.

练习册系列答案
相关题目
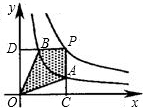 ,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( )
,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( ) 如图,两个反比例函数
如图,两个反比例函数
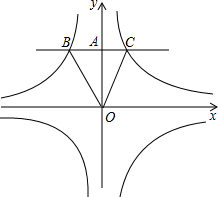 如图,已知反比例函数y=
如图,已知反比例函数y= 已知两个反比例函数
已知两个反比例函数