题目内容
14.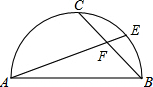 如图,AB是半圆的直径,点C是弧AB的中点,点E是弧BC的中点,连结AE、BC交于点F,则$\frac{EF}{AF}$的值为$\frac{\sqrt{2}-1}{2}$.
如图,AB是半圆的直径,点C是弧AB的中点,点E是弧BC的中点,连结AE、BC交于点F,则$\frac{EF}{AF}$的值为$\frac{\sqrt{2}-1}{2}$.
分析 利用已知首先判断△ACF∽△EHF,进而得出答案.
解答 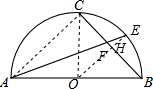 解:如图,设圆心为O,连接OC,AC,OE交BC于点H,
解:如图,设圆心为O,连接OC,AC,OE交BC于点H,
∵点E是弧BC的中点,
∴OE⊥BC,
∵AB是半圆的直径,
∴AC⊥BC
∴EH∥AC,
∴△ACF∽△EHF,
∴$\frac{EF}{AF}=\frac{EH}{AC}$,
∵点C是弧AB的中点,
∴△ABC是等腰直角三角形,
设AC=2x,则OE=OB=$\sqrt{2}$x,
∴OH=x,EH=($\sqrt{2}$-1)x,
∴$\frac{EF}{AF}=\frac{EH}{AC}$=$\frac{\sqrt{2}-1}{2}$.
故答案为:$\frac{\sqrt{2}-1}{2}$.
点评 此题主要考查了相似三角形的判定与性质以及圆周角定理,正确利用圆周角定理得出对应角相等是解题关键.

练习册系列答案
相关题目
13.下列图案中,既是中心对称又是轴对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.分式方程$\frac{1}{x-1}$=1的解为( )
| A. | x=2 | B. | x=1 | C. | x=-1 | D. | x=-2 |
19.如果代数式$\frac{\sqrt{-x}}{x+1}$有意义,则x的取值范围是( )
| A. | x≤0 | B. | x≠-1 | C. | x≤0且x≠-1 | D. | x>-1 |
6.下列运算正确的是( )
| A. | 3a-2a=1 | B. | a3+a2=a5 | C. | (-a)2•a3=a6 | D. | (-a2)3=-a6 |
 如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.
如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.