题目内容
5.△ABC中,若$|{2sinA-\sqrt{3}}|+{(cosB-\frac{1}{2})^2}=0$,则△ABC是等边三角形.分析 先根据非负数的性质求出sinA及cosB的值,再由特殊角的三角函数值得出∠A及∠B的值,进而可判断出△ABC的形状.
解答 解:∵△ABC中,$|{2sinA-\sqrt{3}}|+{(cosB-\frac{1}{2})^2}=0$,
∴sinA=$\frac{\sqrt{3}}{2}$,cosB=$\frac{1}{2}$,
∴∠A=60°,∠B=60°,
∴∠C=180°-60°-60°=60°.
∴△ABC是等边三角形.
故答案为:等边.
点评 本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
13.已知二次函数y=ax2+2ax+c的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是( )
| A. | (1,0) | B. | (-1,0) | C. | (-3,0) | D. | (3,0) |
10.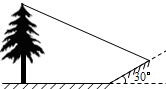 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )| A. | ($6+\sqrt{3}$)米 | B. | 12米 | C. | ($4+2\sqrt{3}$)米 | D. | 10米 |
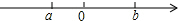 已知实数a,b在数轴上位置如图所示,化简:$\sqrt{{a}^{2}}$+|a-b|=-2a+b.
已知实数a,b在数轴上位置如图所示,化简:$\sqrt{{a}^{2}}$+|a-b|=-2a+b.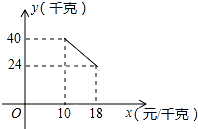 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示: 二次函数y=ax2+bx+c的图象如图所示,则b2-4ac>0(填“>”“<”或“=”)
二次函数y=ax2+bx+c的图象如图所示,则b2-4ac>0(填“>”“<”或“=”)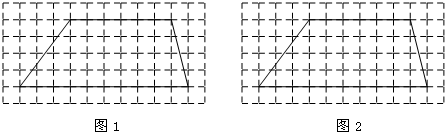
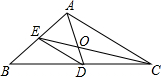 如图,O是△ABC的重心,若△EDO的周长为4,则△AOC的周长为8.
如图,O是△ABC的重心,若△EDO的周长为4,则△AOC的周长为8.