题目内容
13．
如图，∠A+∠B+∠C+∠D+∠E+∠F=360°．
分析 根据三角形内角与外角的关系可得∠E+∠AFE=∠2，∠A+∠B=∠1，再利用四边形内角和为360°可得答案．
解答 
解：延长AF交BC于一点，
∵∠E+∠AFE=∠2，∠A+∠B=∠1，
∴∠A+∠B+∠C+∠D+∠E+∠F=∠2+∠1+∠C+∠D=360°，
故答案为：360°．
点评 此题主要考查了三角形内角与外角的关系，以及四边形内角和，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．
练习册系列答案
相关题目
18．
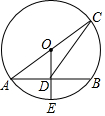如图，AC是⊙O的直径，AB是⊙O的弦，点E是弧AB的中点，连结OE，交AB于点D，再连结CD，若tan∠CDB=$\frac{3}{2}$，则AB与DE的数量关系是（ ）
如图，AC是⊙O的直径，AB是⊙O的弦，点E是弧AB的中点，连结OE，交AB于点D，再连结CD，若tan∠CDB=$\frac{3}{2}$，则AB与DE的数量关系是（ ）| A． | AB=2DE | B． | AB=3DE | C． | AB=4DE | D． | 2AB=3DE |