题目内容
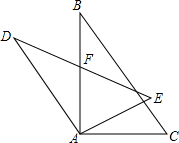如图，三角形ADE是三角形ABC饶点A逆时针旋转30°后所得的图形，若∠D=28°，∠C=52°，AB与DE交于点F．求：∠BAE，∠BFE．考点：全等三角形的判定与性质
专题：
分析：根据旋转的性质知△ABC≌△ADE，∠CAE=∠BAD=30°，则对应角∠C=∠E=52°，由三角形内角和定理知∠DAE=180°-∠D-∠E=100°，所以由图示得到：∠BAE=100°-30°=70°、∠AFD=180°-∠D-∠BAF=122°，根据对顶角相等推知∠BFE=122°
解答：解：∵△ABC饶点A逆时针旋转30°后得到△ADE，
∴△ABC≌△ADE，∠CAE=∠BAD=30°，
∴∠C=∠E．
又∵∠D=28°，∠C=52°，
∴∠E=52°，∠DAE=180°-∠D-∠E=100°，
∠BAE=100°-30°=70°，
∠AFD=180°-∠D-∠BAF=122°，
∴∠BFE=122°（对顶角相等）．
∴△ABC≌△ADE，∠CAE=∠BAD=30°，
∴∠C=∠E．
又∵∠D=28°，∠C=52°，
∴∠E=52°，∠DAE=180°-∠D-∠E=100°，
∠BAE=100°-30°=70°，
∠AFD=180°-∠D-∠BAF=122°，
∴∠BFE=122°（对顶角相等）．
点评：本题考查了旋转的性质，全等三角形的判定与性质．解题时，注意挖掘隐含在题中的已知条件：三角形内角和是180°．
练习册系列答案
相关题目
如图，在△ABC中，AD是△ABC的高，AE是△ABC的角平分线．已知∠BAC=82°，∠C=40°，求∠DAE的大小．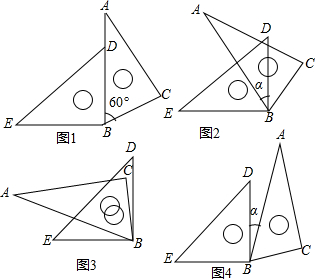
如图1是一副三角尺拼成的图案，三角尺的3个角的顶点是A、C、B，记作“三角尺ACB”；三角尺的3个角的顶点是E、B、D，记作“三角尺EBD”，且∠ACB=∠EBD=90°，∠A=30°，∠ABC=60°，∠E=∠EDB=45°．