题目内容
14. 如图,在平面直角坐标系中,点A的坐标(-2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为$\frac{1}{4}$π.
如图,在平面直角坐标系中,点A的坐标(-2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为$\frac{1}{4}$π.
分析 根据点A的坐标(-2,0),可得OA=2,再根据含30°的直角三角形的性质可得OB的长,再根据性质的性质和扇形的面积公式即可求解.
解答 解:∵点A的坐标(-2,0),
∴OA=2,
∵△ABO是直角三角形,∠AOB=60°,
∴∠OAB=30°,
∴OB=$\frac{1}{2}$OA=1,
∴边OB扫过的面积为:$\frac{90×π×{1}^{2}}{360}$=$\frac{1}{4}$π.
故答案为:$\frac{1}{4}$π.
点评 本题考查了扇形的面积公式:S=$\frac{nπ{R}^{2}}{360}$,其中n为扇形的圆心角的度数,R为圆的半径),或S=$\frac{1}{2}$lR,l为扇形的弧长,R为半径.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
5. 如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
 如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )| A. | ∠ABC=90° | B. | AC=BD | C. | OA=OB | D. | OA=AD |
2.某中学九年级舞蹈兴趣小组8名学生的身高分别为(单位:cm):168,165,168,166,170,170,176,170,则下列说法错误的是( )
| A. | 这组数据的众数是170 | |
| B. | 这组数据的中位数是169 | |
| C. | 这组数据的平均数是169 | |
| D. | 若从8名学生中任选1名学生参加校文艺会演,则这名学生的身高不低于170的概率为$\frac{1}{2}$ |
6.二次函数y=-x2+2x+4的最大值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
3.如果一个多边形的每一个外角都是60°,则这个多边形的边数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
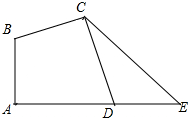 如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.
如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB. 如图,转盘中8个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,指针指向大于6的数的概率为$\frac{1}{4}$.
如图,转盘中8个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,指针指向大于6的数的概率为$\frac{1}{4}$.