题目内容
14.已知a、b、c是△ABC的三条边长.若a、b、c满足a2+$\frac{1}{4}$b2+5=4a+b-|c-2|,试判断△ABC的形状,并说明你的理由.分析 首先利用完全平方公式把a2+$\frac{1}{4}$b2+5=4a+b-|c-2|,化为(a-2)2+($\frac{1}{2}$b-1)2+c-2|=0,利用非负数的性质得出a、b、c的数值,进一步判定即可.
解答 解:△ABC为等边三角形.
∵a2+$\frac{1}{4}$b2+5=4a+b-|c-2|,
∴a2+$\frac{1}{4}$b2+5-4a-b+|c-2|=0,
∴(a-2)2+($\frac{1}{2}$b-1)2+c-2|=0,
∴a-2=0,$\frac{1}{2}$b-1=0,c-2=0,
∴a=b=2,
∴△ABC为等边三角形.
点评 此题考查因式分解的实际运用,非负数的性质,利用完全平方公式因式分解是解决问题的关键.

练习册系列答案
相关题目
4.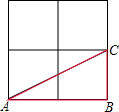 如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )
如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )
 如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )
如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
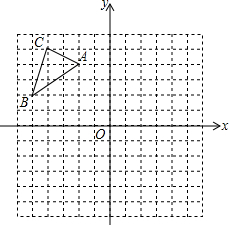 已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移4个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度)
已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移4个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度)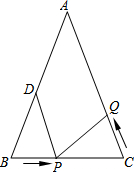 如图所示,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由B出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为t秒.
如图所示,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由B出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为t秒.