题目内容
18.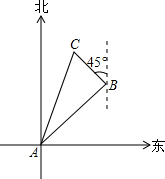 如图,在一次实践活动中,聪聪从A地出发,沿北偏东45°方向行进了4$\sqrt{3}$千米到达B地,然后再沿北偏西45°方向行进了4km到达目的地点C.
如图,在一次实践活动中,聪聪从A地出发,沿北偏东45°方向行进了4$\sqrt{3}$千米到达B地,然后再沿北偏西45°方向行进了4km到达目的地点C.(1)求A、C两地之间的距离;
(2)试确定目的地C在点A的什么方向?
分析 (1)根据图形和题意可得出△ABC为直角三角形,在这个直角三角形中,有AB,BC的值,根据勾股定理可得出AC的值;
(2)在直角三角形ABC中根据三角函数求出∠CAB的值,CA与y轴(北方)的夹角就能求出来了.
解答 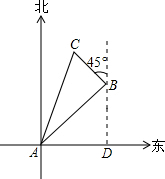 解:(1)如图,作南北方向的平行线BD,交A点的正东方向于点D.
解:(1)如图,作南北方向的平行线BD,交A点的正东方向于点D.
∵∠BAD=45°,
∴∠ABD=45°,
∴∠ABC=180-45-45=90°,
∴△ABC为直角三角形.
在Rt△ABC中,由勾股定理得
AC2=AB2+BC2=(4$\sqrt{3}$)2+42=64,
∴AC=8(千米),
即A、C两地之间的距离为8千米;
(2)直角三角形ABC中,
∵tan∠CAB=BC:AB=4:4$\sqrt{3}$=$\frac{\sqrt{3}}{3}$,
∴∠CAB=30°,
45°-30°=15°.
即目的地C在点A的北偏东15°方向.
点评 本题考查了解直角三角形的应用-方向角问题,按南北方向与东西方向垂直构造直角三角形是比较常用的方法.根据方向角的定义得出△ABC为直角三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
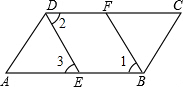 已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC.且∠1=∠3.
已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC.且∠1=∠3.